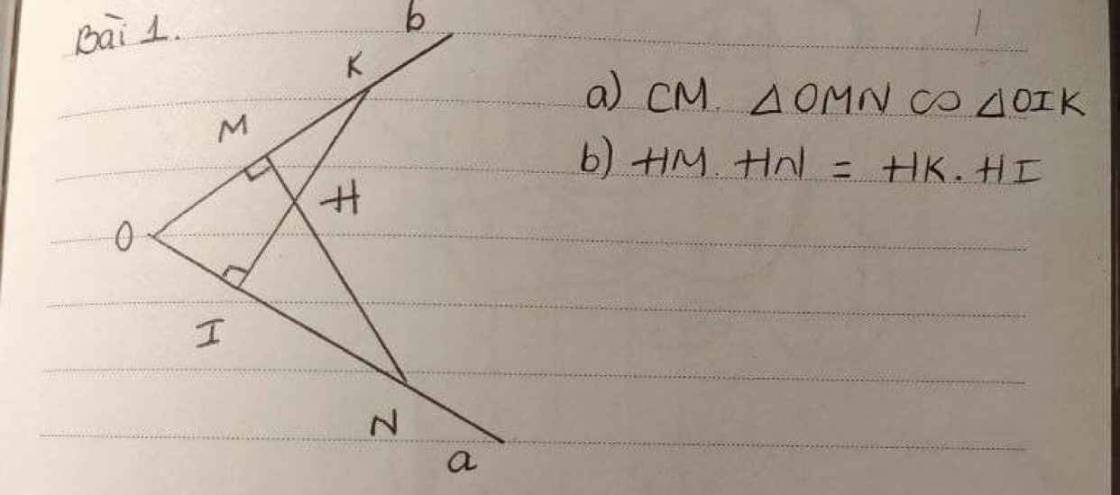a) Xét \(\Delta OMN\) và \(\Delta OIK\) có: \(\left\{{}\begin{matrix}\widehat{O}:chung\\\widehat{OMN}=\widehat{OIK}\left(=90^o\right)\end{matrix}\right.\)
\(\Rightarrow\Delta OMN~\Delta OIK\left(\text{đ}pcm\right)\)
b) Xét \(\Delta MHK\) và \(\Delta IHN\) có: \(\left\{{}\begin{matrix}\widehat{MHK}=\widehat{IHN}\left(\text{đối đỉnh}\right)\\\widehat{HMK}=\widehat{HIN}\left(=90^o\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MHK~\Delta IHN\\ \Rightarrow\dfrac{HM}{HK}=\dfrac{HI}{HN}\\ \Rightarrow HM.HN=HI.HK\left(\text{đ}pcm\right)\)
a: Xét ΔOMN vuông tại M và ΔOIK vuông tại I có
góc MON chung
=>ΔOMN đồng dạng với ΔOIK
b: Xét ΔHIN vuông tại I và ΔHMK vuông tại M có
góc IHN=góc MHK
=>ΔHIN đồng dạg với ΔHMK
=>HI/HM=HN/HK
=>HI*HK=HM*HN