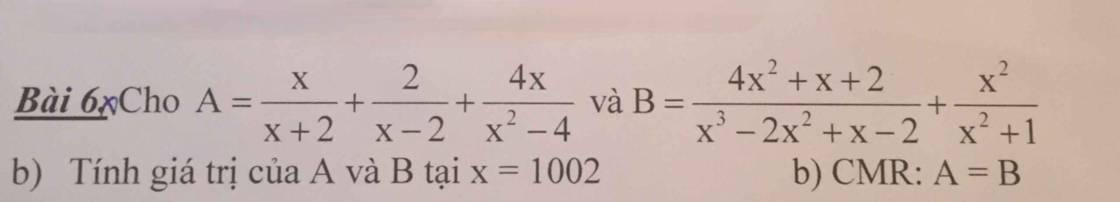a)
A\(=\dfrac{x}{x+2}+\dfrac{2}{x-2}+\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-2x+2x+4+4x}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x+2}{x-2}\)
với x=1002 thì
\(\dfrac{1002+2}{1002-2}=\dfrac{251}{250}\)
\(B=\dfrac{4x^2+x+2}{x^2\left(x-2\right)+\left(x-2\right)}+\dfrac{x^2}{x^2+1}\\ =\dfrac{4x^2+x+2}{\left(x-2\right)\left(x^2+1\right)}+\dfrac{x^2}{x^2+1}\\ =\dfrac{4x^2+x+2}{\left(x-2\right)\left(x^2+1\right)}+\dfrac{x^2\left(x-2\right)}{\left(x^2+1\right)\left(x-2\right)}\\ =\dfrac{4x^2+x+2+x^3-2x^2}{\left(x^2+1\right)\left(x-2\right)}\\ =\dfrac{x^3+2x^2+x+2}{\left(x^2+1\right)\left(x-2\right)}\\ =\dfrac{x^2\left(x+2\right)+\left(x+2\right)}{\left(x^2+1\right)\left(x-2\right)}\\ =\dfrac{\left(x+2\right)\left(x^2+1\right)}{\left(x^2+1\right)\left(x-2\right)}\\ =\dfrac{x+2}{x-2}\)
với x=1002 thì
\(\dfrac{1002+2}{1002-2}=\dfrac{251}{250}\)
b)
vì \(\dfrac{x+2}{x-2}=\dfrac{x+2}{x-2}\) nên A=B