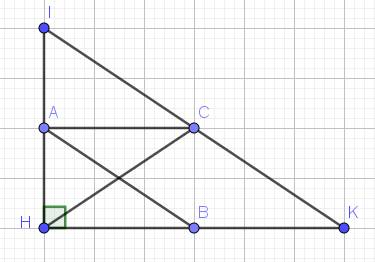
a: Xét ΔHKI có HA/HI=HB/HK
nên AB//IK và AB=IK/2
=>ABKI là hình bình hành
b: Xét tứ giác ABKC có
AB//KC
AB=KC
DO đo: ABKC là hình bình hành
c: HC=KI/2=5cm
Lời giải:
a.
Vì $A, B$ lần lượt là trung điểm của $HI, HK$ nên $AB$ là đường trung bình của tam giác $HIK$ ứng với cạnh $IK$
$\Rightarrow AB\parallel IK$
$\Rightarrow ABKI$ là hình thang
b.
$AB$ là đường trung bình ứng với cạnh $IK$ (cmt)
$\Rightarrow AB\parallel IK$ và $AB=\frac{1}{2}KI$
$\Leftrightarrow AB\parallel KC$ và $AB=KC$
$\Rightarrow ABKC$ là hình bình hành
c.
Tam giác $HIK$ là tam giác vuông nên đường trung tuyến $HC$ ứng với cạnh huyền $IK$ bằng một nửa cạnh huyền.
Tức là $HC=\frac{1}{2}IK=5$ (cm)