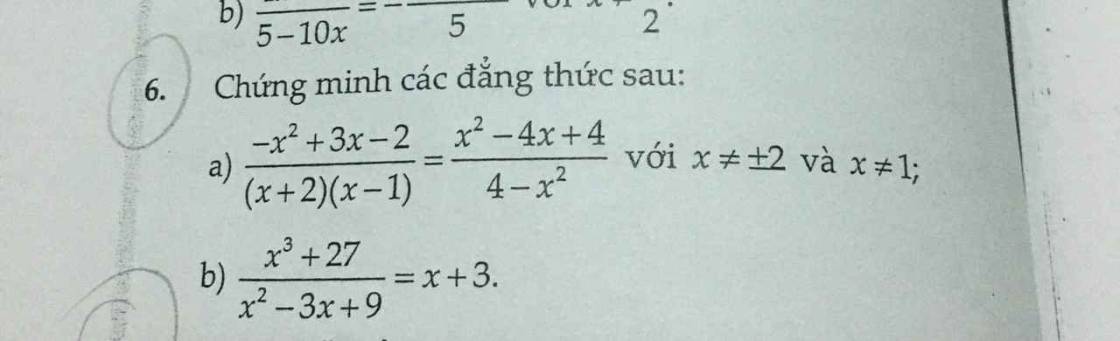`a)` Với `x \ne +-2;x \ne 1` có:
`VT=[-x^2+3x-2]/[(x+2)(x-1)]=[-x^2+x+2x-2]/[(x+2)(x-1)]`
`=[(2-x)(x-1)]/[(x+2)(x-1)]=[2-x]/[x+2]`
`VP=[x^2-4x+4]/[4-x^2]=[(x-2)^2]/[(2-x)(x+2)]=[2-x]/[x+2]=VT`
`=>Đpcm`
`b)VT=[x^3+27]/[x^2-3x+9]=[(x+3)(x^2-3x+9)]/[x^2-3x+9]=x+3=VP`
`=>Đpcm`
\(a,VT=\dfrac{-x^2+3x-2}{\left(x+2\right)\left(x-1\right)}\\ =\dfrac{-\left(x^2-3x+2\right)}{\left(x+2\right)\left(x-1\right)}\\ =\dfrac{-\left(x^2-x-2x+2\right)}{\left(x+2\right)\left(x-1\right)}\\ =\dfrac{-\left[x\left(x-1\right)-2\left(x-1\right)\right]}{\left(x+2\right)\left(x-1\right)}\\ =\dfrac{-\left(x-2\right)\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}\\ =\dfrac{-\left(x-2\right)}{x+2}\\ =\dfrac{-\left(x-2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{-\left(x-2\right)^2}{x^2-4}\\ =\dfrac{x^2-4x+4}{4-x^2}=VP\left(đpcm\right)\)
\(b,VT=\dfrac{x^3+27}{x^2-3x+9}\\ =\dfrac{\left(x+3\right)\left(x^2-3x+9\right)}{x^2-3x+9}\\ =x+3=VP\left(đpcm\right)\)