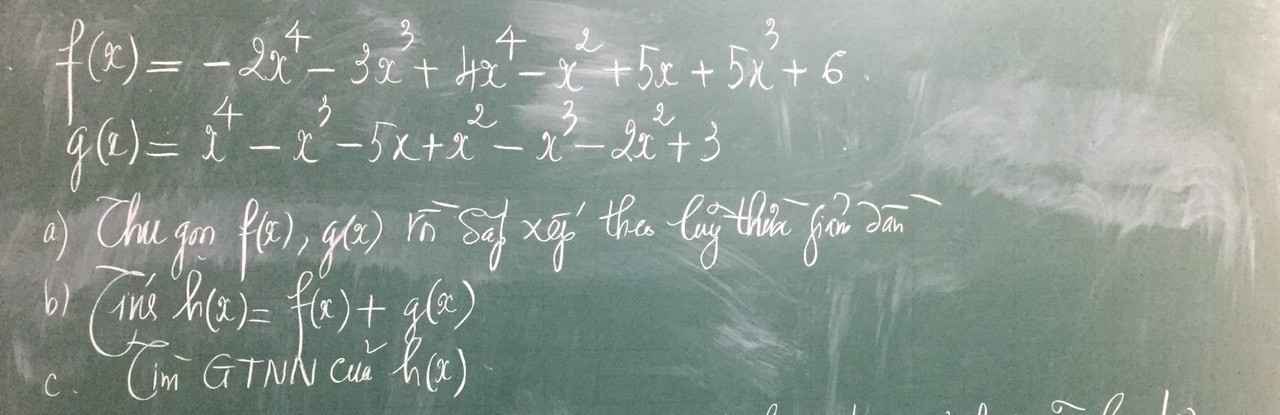a: \(f\left(x\right)=2x^4+2x^3-x^2+5x+6\)
\(g\left(x\right)=x^4-2x^3-x^2-5x+3\)
b: \(h\left(x\right)=f\left(x\right)+g\left(x\right)=3x^4+9\)
c: h(x)>=9 với mọi x
Dấu '=' xảy ra khi x=0
a) $f(x) = 2x^4 + 2x^3 -x^2 + 5x + 6$
$g(x) = x^4 - 2x^3 - x^2 - 5x + 3$
b) $h(x) = f(x) + g(x) = 2x^4 + 2x^3 -x^2 + 5x + 6 + x^4 - 2x^3 - x^2 - 5x + 3$
$= 3x^4 - 2x^2 + 9$
c)
$h(x) = 3(x^4 - \dfrac{2}{3}x^2 + 3) = 3(x^4 - \dfrac{2}{3}x^2 + \dfrac{1}{9} - \dfrac{1}{9} + 3) = 3(x^2 - \dfrac{1}{3})^2 + \dfrac{26}{3}$
Vì $3(x^2 - \dfrac{1}{3} )^2 ≥ 0$ với mọi x nên $h(x) ≥ \dfrac{26}{3}$
Vậy GTNN của h(x) là $\dfrac{26}{3}$