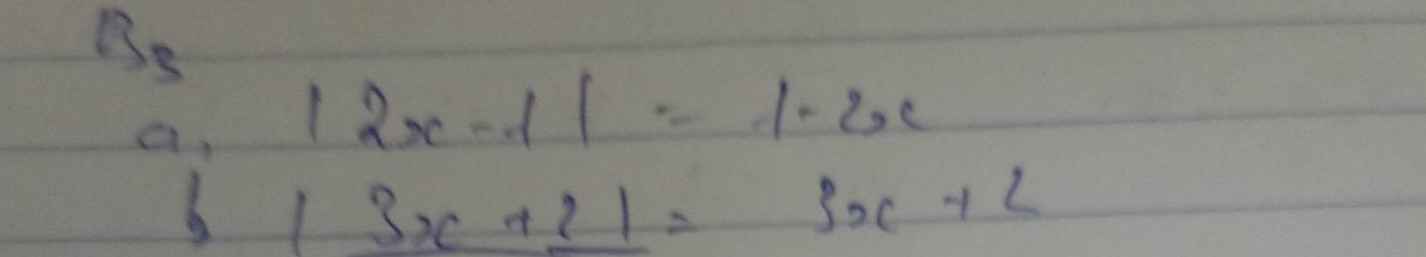a: |2x-1|=1+2x
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{1}{2}\\\left(2x+1-2x+1\right)\left(2x+1+2x-1\right)=0\end{matrix}\right.\Leftrightarrow x=0\)
b: |3x+2|=3x+2
=>3x+2>=0
hay x>=-2/3
a)\(\left|2x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=1-2x\\2x-1=-\left(1-2x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1-1+2x=0\\2x-1=-1+2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-2=0\\2x-1=2x-1\left(luôn-đúng\right)\end{matrix}\right.\)`∀x ∈R`
`=>4x-2=0`
`<=> x =1/2 `
b)\(\left|3x+2\right|=3x+2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=3x+2\left(luôn-đúng\right)\\3x+2=-3x-2\end{matrix}\right.\)`∀x ∈R`
`=>3x+2=-3x-2`
`<=>3x+2+3x+2=0`
`<=> 6x +4 =0`
`<=> 6x=-4`
`<=> x=-2/3 `