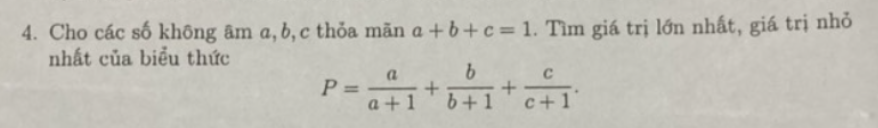\(P=\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}=-\left(1-\dfrac{a}{a+1}+1-\dfrac{b}{b+1}+1-\dfrac{c}{c+1}\right)+3=-\left(\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\right)+3\)-Áp dụng BĐT Caushy-Schwarz ta có:
\(P=-\left(\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\right)+3\le-\dfrac{\left(1+1+1\right)^2}{a+b+c+1+1+1}+3\le-\dfrac{9}{4}+3=\dfrac{3}{4}\)\(P=\dfrac{3}{4}\Leftrightarrow a=b=c=\dfrac{1}{3}\)
-Vậy \(P_{max}=\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
