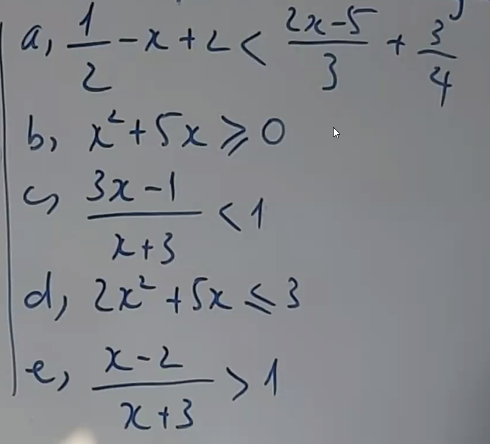\(a,\dfrac{1}{2}-x+2< \dfrac{2x-5}{3}+\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{2}-x+2-\dfrac{2x-5}{3}-\dfrac{3}{4}< 0\)
\(\Leftrightarrow\dfrac{6-12x+24-4\left(2x-5\right)-9}{12}< 0\)
\(\Leftrightarrow6-12x+24-8x+20-9< 0\)
\(\Leftrightarrow-20x+41< 0\)
\(\Leftrightarrow-20x< -41\)
\(\Leftrightarrow x>\dfrac{41}{20}\)
\(b,x^2+5x\ge0\)
\(\Leftrightarrow x\left(x+5\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x+5\ge0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x\ge-5\end{matrix}\right.\)
\(c,\dfrac{3x-1}{x+3}< 1\)
\(\Leftrightarrow\dfrac{3x-1}{x+3}-1< 0\)
\(\Leftrightarrow\dfrac{3x-1-x-3}{x+3}< 0\)
\(\Leftrightarrow2x-4< 0\)
\(\Leftrightarrow2x< 4\)
\(\Leftrightarrow x< 2\)
-Đối với phương trình bậc 2 (3,4...) hoặc phương trình chứa ẩn ở mẫu thì bạn phải xét đủ trường hợp:
d) \(2x^2+5x\le3\)
\(\Leftrightarrow2x^2+5x-3\le0\)
\(\Leftrightarrow2x^2+6x-x-3\le0\)
\(\Leftrightarrow2x\left(x+3\right)-\left(x+3\right)\le0\)
\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3\le0\\2x-1\ge0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x+3\ge0\\2x-1\le0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-3\\x\ge\dfrac{1}{2}\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x\ge-3\\x\le\dfrac{1}{2}\end{matrix}\right.\) (có thể xảy ra)
-Vậy tập nghiệm của BPT là \(-3\le x\le\dfrac{1}{2}\)
e) \(\dfrac{x-2}{x+3}>1\)
\(\Leftrightarrow\dfrac{x-2}{x+3}-1>0\)
\(\Leftrightarrow\dfrac{x-2-x-3}{x+3}>0\)
\(\Leftrightarrow\dfrac{-5}{x+3}>0\)
\(\Leftrightarrow x+3< 0\)
\(\Leftrightarrow x< -3\)
-Vậy nghiệm của BPT là x<-3
c. \(\dfrac{3x-1}{x+3}< 1\)
\(\Leftrightarrow\dfrac{3x-1}{x+3}-1< 0\)
\(\Leftrightarrow\dfrac{3x-1-x-3}{x+3}< 0\)
\(\Leftrightarrow\dfrac{2x-4}{x+3}< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-4< 0\\x+3>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}2x-4>0\\x+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 2\\x>-3\end{matrix}\right.\) (có thể xảy ra) hay \(\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\) (vô lý)
-Vậy nghiệm của BPT là \(-3< x< 2\)