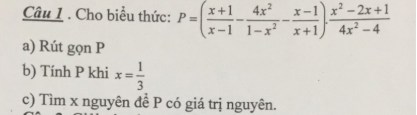a, ĐK: \(x\ne\pm1\)
\(P=\left(\dfrac{x+1}{x-1}-\dfrac{4x^2}{1-x^2}-\dfrac{x-1}{x+1}\right).\dfrac{x^2-2x+1}{4x^2-4}\)
\(=\left[\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4x^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\right].\dfrac{\left(x-1\right)^2}{4\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+2x+1+4x^2-x^2+2x-1}{\left(x-1\right)\left(x+1\right)}.\dfrac{x-1}{4\left(x+1\right)}\)
\(=\dfrac{4x^2+4x}{x+1}.\dfrac{1}{4\left(x+1\right)}\)
\(=\dfrac{4x\left(x+1\right)}{x+1}.\dfrac{1}{4\left(x+1\right)}\)
\(=\dfrac{x}{x+1}\)
b, \(P=\dfrac{x}{x+1}=\dfrac{\dfrac{1}{3}}{\dfrac{1}{3}+1}=\dfrac{\dfrac{1}{3}}{\dfrac{4}{3}}=\dfrac{1}{4}\)
a)ĐKXĐ: \(x\ne\pm1\)
\(P=\left(\dfrac{x+1}{x-1}-\dfrac{4x^2}{1-x^2}-\dfrac{x-1}{x+1}\right).\dfrac{x^2-2x+1}{4x^2-4}\)
\(=\left[\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4x^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}\right].\dfrac{\left(x-1\right)^2}{4\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+2x+1+4x^2-x^2+2x-1}{\left(x-1\right)\left(x+1\right)}.\dfrac{x-1}{4\left(x+1\right)}\)
\(=\dfrac{4x^2+4x}{\left(x-1\right)\left(x+1\right)}.\dfrac{x-1}{4\left(x+1\right)}\)
\(=\dfrac{4x\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}.\dfrac{x-1}{4\left(x+1\right)}\)
\(=\dfrac{x}{x+1}\)
b) Tại x= \(\dfrac{1}{3}\) giá trị của biểu thức P là :
\(P=\dfrac{\dfrac{1}{3}}{\dfrac{1}{3}+1}=\dfrac{1}{3}:\dfrac{4}{3}=\dfrac{1}{4}\)
c) Để P có giá trị nguyên thì :
\(\begin{matrix} x⋮x+1\\x+1⋮x+1\end{matrix}\) \(\Leftrightarrow x-x-1⋮x+1\) \(\Leftrightarrow-1⋮x+1\)
\(\Rightarrow x+1\inƯ\left(-1\right)=\left\{\pm1\right\}\)
Ta có bảng sau :
| x+1 | 1 | -1 |
| x | 0 | -2 |
Vậy...
c, \(P\in Z\Leftrightarrow\dfrac{x}{x+1}\in Z\)
\(\Leftrightarrow1-\dfrac{1}{x+1}\in Z\)
\(\Leftrightarrow x+1\in\left\{\pm1\right\}\)
\(\Leftrightarrow x\in\left\{-2;0\right\}\)