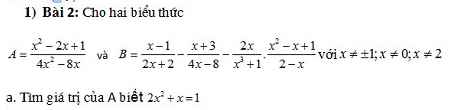a: \(2x^2+x-1=0\)
=>(2x+1)(x-1)=0
=>x=-1/2 hoặc x=1
Thay x=1 vào A, ta được:
\(A=\dfrac{\left(1-1\right)^2}{4\cdot1\cdot\left(1-2\right)}=0\)
Thay x=-1/2 vào A, ta được:
\(A=\dfrac{\left(-\dfrac{1}{2}-1\right)^2}{4\cdot\dfrac{-1}{2}\cdot\left(-\dfrac{1}{2}-2\right)}=\dfrac{9}{20}\)
\(2x^2+x=1\\ \Rightarrow2x^2+x-1=0\\ \Rightarrow\left(2x^2+2x\right)-\left(x+1\right)=0\\ \Rightarrow2x\left(x+1\right)-\left(x+1\right)=0\\ \Rightarrow\left(x+1\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Thay x=-1 vào A ta có:
\(A=\dfrac{x^2-2x+1}{4x^2-8x}=\dfrac{\left(-1\right)^2-2\left(-1\right)+1}{4\left(-1\right)^2-8\left(-1\right)}=\dfrac{1}{3}\)
Thay x=\(\dfrac{1}{2}\) vào A ta có:
\(A=\dfrac{x^2-2x+1}{4x^2-8x}=\dfrac{\left(\dfrac{1}{2}\right)^2-2.\dfrac{1}{2}+1}{4\left(\dfrac{1}{2}\right)^2-8.\dfrac{1}{2}}=\dfrac{-1}{12}\)