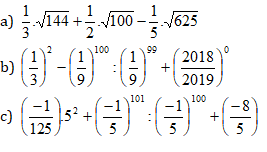a: \(=\dfrac{1}{3}\cdot12+\dfrac{1}{2}\cdot10-\dfrac{1}{5}\cdot25=4+5-5=4\)
b: \(=\dfrac{1}{9}-\dfrac{1}{9}+1=1\)
\(\text{a)}\dfrac{1}{3}.\sqrt{144}+\dfrac{1}{2}.\sqrt{100}-\dfrac{1}{5}.\sqrt{625}\)
\(=\dfrac{1}{3}.12+\dfrac{1}{2}.10-\dfrac{1}{5}.25\)
\(=4+5-5\)
\(=9-5\)
\(=4\)
\(\text{b)}\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{9}\right)^{100}:\left(\dfrac{1}{9}\right)^{99}+\left(\dfrac{2018}{2019}\right)^0\)
\(=\dfrac{1}{9}-\dfrac{1}{9}+1\)
\(=0+1\)
\(=1\)
\(\text{c)}\left(\dfrac{-1}{125}\right).5^2+\left(\dfrac{-1}{5}\right)^{101}:\left(\dfrac{-1}{5}\right)^{100}+\left(\dfrac{-8}{5}\right)\)
\(=\left(\dfrac{-1}{125}\right).25+\left(\dfrac{-1}{5}\right)+\left(\dfrac{-8}{5}\right)\)
\(=\left(\dfrac{-1}{5}\right)+\left(\dfrac{-1}{5}\right)+\left(\dfrac{-8}{5}\right)\)
\(=\left(\dfrac{-2}{5}\right)+\left(\dfrac{-8}{5}\right)\)
\(=\left(\dfrac{-10}{5}\right)=-2\)