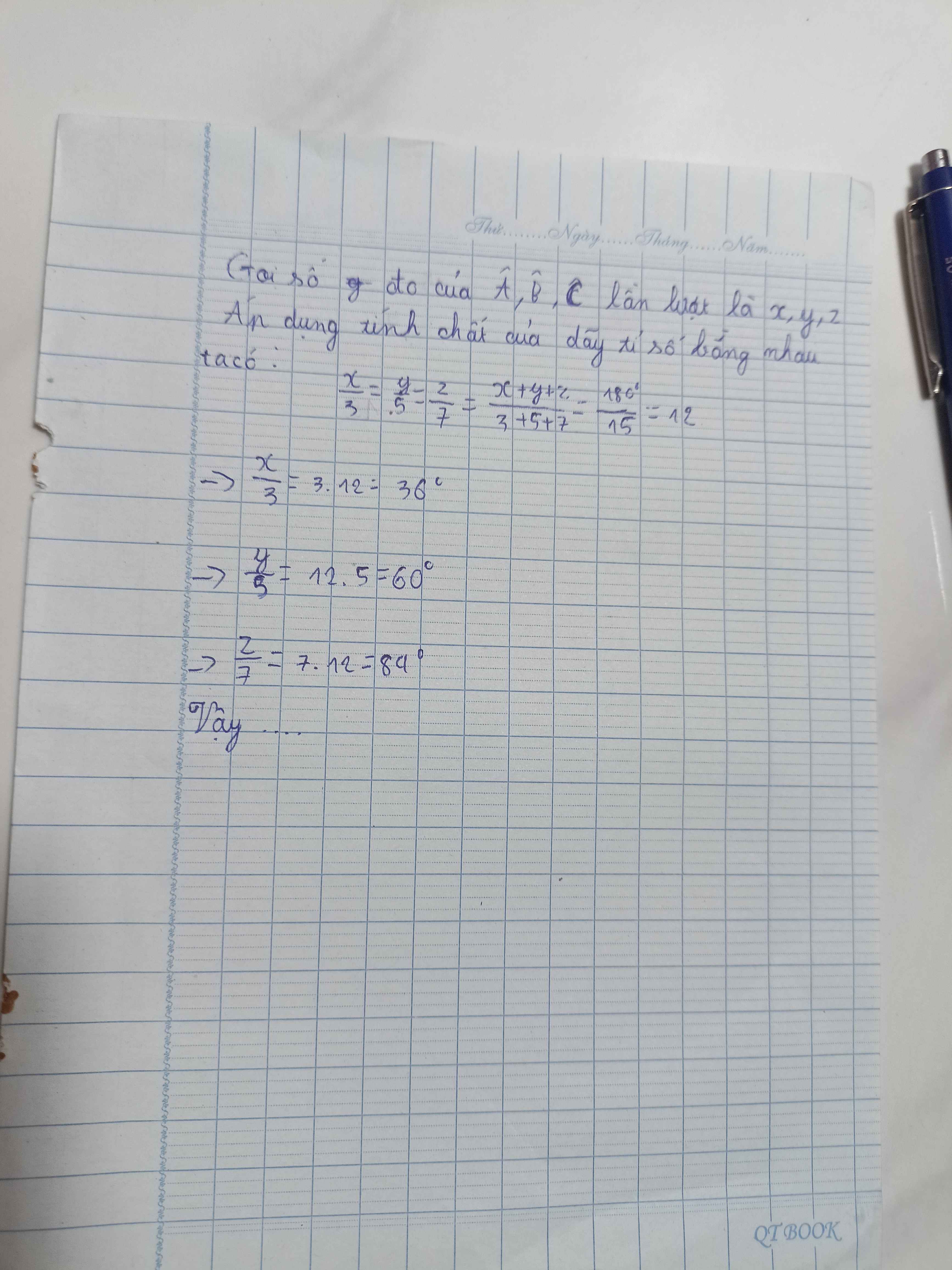Gọi số đo góc A,B,C lần lượt là a,b,c(a,b,c>0)
Áp dụng t/c dtsbn ta có:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)
\(\dfrac{\widehat{A}}{3}=12^o\Rightarrow\text{}\text{}\widehat{A}=36^o\\ \dfrac{\widehat{B}}{5}=12^o\Rightarrow\widehat{B}=60^o\\ \dfrac{\widehat{C}}{7}=12^o\Rightarrow\widehat{C}=84^o\)
Ta gọi lần lượt số đo các góc của tam giác ABC là a, b, c
Ta có 3 góc tam giác ABC tỉ lệ vs 3; 5; 7
=> \(\dfrac{a}{3}\) = \(\dfrac{b}{5}\) = \(\dfrac{c}{7}\) và a + b + c = 180°
Theo tính chất dãy tỉ số bằng nhau
\(\dfrac{a}{3}\) = \(\dfrac{b}{5}\) = \(\dfrac{c}{7}\) = \(\dfrac{a+b+c}{3+5+7}\) = \(\dfrac{180}{15}\) = 12
\(\dfrac{a}{3}\) = 12 => a = 12.3 = 36
\(\dfrac{b}{5}\) = 12 => b = 12.5 = 60
\(\dfrac{c}{7}\) = 12 => c = 12.7 = 84
Vậy A = 36; B= 60; C= 84