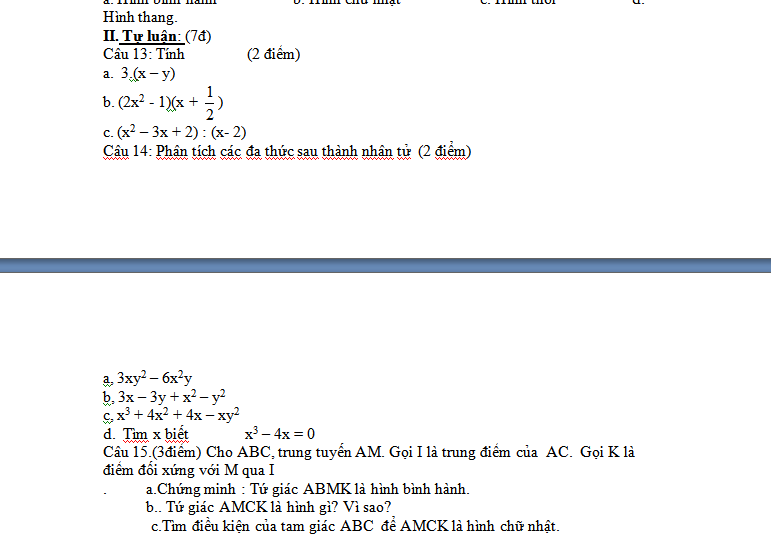
Câu 13:
a. $3(x-y)=3x-3y$
b. $(2x^2-1)(x+\frac{1}{2})=2x^3+x^2-x-\frac{1}{2}$
c.
$(x^2-3x+2):(x-2)=[(x-1)(x-2)]:(x-2)=x-1$
Câu 14:
a. $3xy^2-6x^2y=3xy(y-2x)$
b. $3x-3y+x^2-y^2=3(x-y)+(x-y)(x+y)=(x-y)(3+x+y)$
c. $x^3+4x^2+4x-xy^2=x(x^2+4x+4-y^2)$
$=x[(x^2+4x+4)-y^2]=x[(x+2)^2-y^2]=x(x+2-y)(x+2+y)$
d.
$x^3-4x=0$
$\Leftrightarrow x(x^2-4)=0$
$\Leftrightarrow x(x-2)(x+2)=0$
$\Rightarrow x=0$ hoặc $x-2=0$ hoặc $x+2=0$
$\Leftrightarrow x=0$ hoặc $x=\pm 2$
câu 13
a) \(3\left(x-y\right)=3x-3y\)
b) \(\left(2x^2-1\right)\left(x+\dfrac{1}{2}\right)=2x^3+x^2-x-\dfrac{1}{2}\)
c) \(\left(x^2-3x+2\right):\left(x-2\right)=\left(x-1\right)\left(x-2\right):\left(x-2\right)=x-1\)
Câu 15
a. Vì AM là trung tuyến
=> M là trung điểm BC
I là trung điểm AC
=> IM là đường trung bình của tam giác ABC
=> IM // AB; IM = \(\dfrac{1}{2}\) AB
mà I là trung điểm MK (K đối xứng với M qua I) => MK = AB
Xét tứ giác ABMK có: MK // AB (MI // AB)
MK = AB (cmt)
=> tứ giác ABMK là hình bình hành
b) Xét tứ giác AMCK có : I là trung điểm AC (gt)
I là trung điểm MK (K đối xứng với M qua I)
=> tứ giác AMCK là hình bình hành
c) hình bình hành AMCK là hình chữ nhật ⇔ góc AMC = 90 độ
=> AM là đường cao mà AM là trung tuyến
Tam giác ABC cân tại A
Vậy tam giác ABC cân tại A thì tứ giác AMCK là hình chữ nhật
Câu 15:
a.
$K$ đối xứng $M$ qua $I$ tức là $I$ là trung điểm $KM$
Tứ giác $AKCM$ có 2 đường chéo cắt nhau tại trung điểm $I$ của mỗi đường nên $AKCM$ là hình bình hành
$\Rightarrow AK=MC$ và $AK\parallel MC$
$\Rightarrow AK=BM$ và $AK\parallel BM$
Tứ giác $AKMB$ có cặp cạnh đối $AK, BM$ song song và bằng nhau nên $AKMB$ là hình bình hành.
b. Đã cm ở phần a.
c. Để $AMCK$ là hình chữ nhật thì $\widehat{AMC}=90^0$
$\Leftrightarrow AM$ vừa là đường trung tuyến vừa là đường cao
$\Leftrightarrow ABC$ là tam giác cân tại $A$