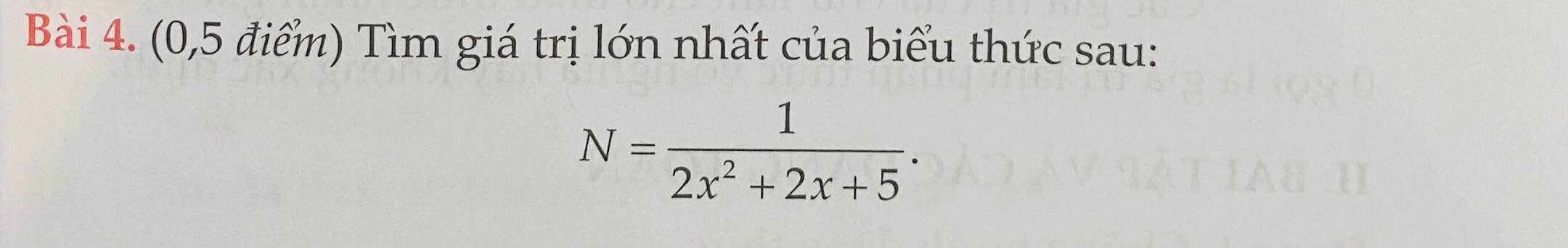Question

Answer 1

\(2x^2+2x+5=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{9}{2}=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{9}{2}\ge\dfrac{9}{2}\)

\(\Rightarrow N=\dfrac{1}{2x^2+2x+5}\le\dfrac{1}{\dfrac{9}{2}}=\dfrac{2}{9}\)

\(maxN=\dfrac{2}{9}\Leftrightarrow x=-\dfrac{1}{2}\)

Answer 2

\(N=\dfrac{1}{2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{9}{2}}=\dfrac{1}{2\left(x+\dfrac{1}{2}\right)^2+\dfrac{9}{2}}\le\dfrac{1}{0+\dfrac{9}{2}}=\dfrac{2}{9}\\ N_{max}=\dfrac{2}{9}\Leftrightarrow x=-\dfrac{1}{2}\)