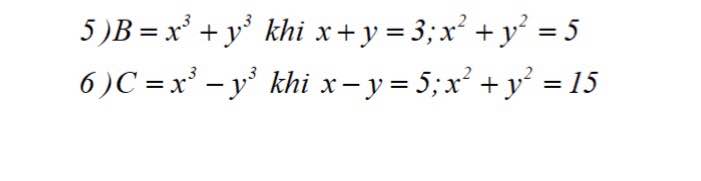5: Ta có: \(x+y=3\)
nên \(\left(x+y\right)^2=9\)
\(\Leftrightarrow x^2+y^2+2xy=9\)
\(\Leftrightarrow2xy+25=9\)
hay xy=-8
\(B=x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=3^3-3\cdot\left(-8\right)\cdot3\)
\(=27+9\cdot8=99\)
Lời giải:
5. $xy=\frac{(x+y)^2-(x^2+y^2)}{2}=\frac{3^2-5}{2}=2$
$B=x^3+y^3=(x+y)(x^2-xy+y^2)=3(5-2)=9$
6.
$xy=\frac{x^2+y^2-(x-y)^2}{2}=\frac{15-5^2}{2}=-5$
$C=x^3-y^3=(x-y)(x^2+xy+y^2)=5(15-5)=50$