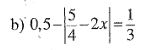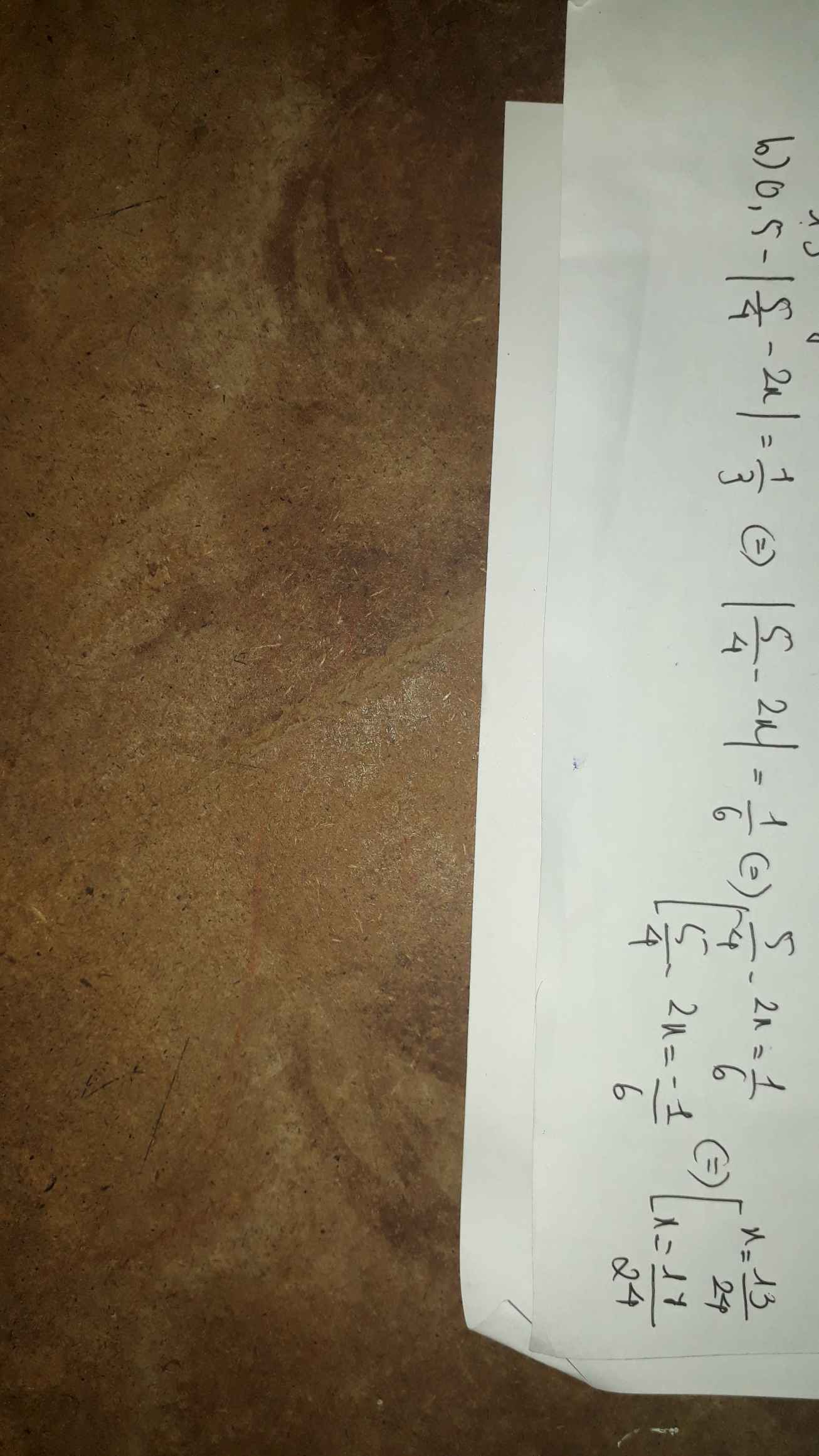\(0,5-\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{3}\)
\(-\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{3}-0,5\)
\(-\left|\dfrac{5}{4}-2x\right|=-\dfrac{1}{6}\)
\(\left|\dfrac{5}{4}-2x\right|.\left(-1\right)=\dfrac{1}{6}.\left(-1\right)\)
\(\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{6}\)
\(\dfrac{5}{4}-2x=\dfrac{1}{6}\)hoặc \(-\left(\dfrac{5}{4}-2x\right)=\dfrac{1}{6}\)
\(-2x=\dfrac{1}{6}-\dfrac{5}{4}\)hoặc \(-\dfrac{5}{4}+2x=\dfrac{1}{6}\)
\(-2x=-\dfrac{13}{12}\)hoặc \(2x=\dfrac{1}{6}+\dfrac{5}{4}\)
\(x=\dfrac{13}{24}\)hoặc \(2x=\dfrac{17}{12}\)
\(x=\dfrac{13}{24}\)hoặc \(x=\dfrac{17}{24}\)
Ta có: \(\dfrac{1}{2}-\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{3}\)
\(\Leftrightarrow\left|2x-\dfrac{5}{4}\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{5}{4}=\dfrac{1}{6}\\2x-\dfrac{5}{4}=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{17}{12}\\2x=\dfrac{13}{12}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{17}{24}\\x=\dfrac{13}{24}\end{matrix}\right.\)