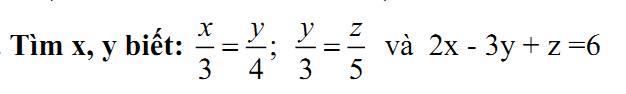Ta có: \(\dfrac{x}{3}=\dfrac{y}{4};\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{x}{36}=\dfrac{y}{48};\dfrac{y}{48}=\dfrac{z}{80}\)
⇒\(\dfrac{2x}{72}=\dfrac{3y}{144}=\dfrac{z}{80}\) ⇒\(\dfrac{2x-3y+z}{72-144+80}=\dfrac{3}{4}\)
\(\dfrac{x}{3}=\dfrac{3}{4}\Rightarrow x=\dfrac{9}{4}\)
\(\dfrac{y}{4}=\dfrac{3}{4}\Rightarrow y=3\)
\(\dfrac{z}{5}=\dfrac{3}{4}\Rightarrow z=\dfrac{15}{4}\)
Ta có: \(\dfrac{x}{3}=\dfrac{y}{4}\)
nên \(\dfrac{x}{9}=\dfrac{y}{12}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{20}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
hay \(\dfrac{2x}{18}=\dfrac{3y}{36}=\dfrac{z}{20}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{18}=\dfrac{3y}{36}=\dfrac{z}{20}=\dfrac{2x-3y+z}{18-36+20}=\dfrac{6}{2}=3\)
Do đó: \(\left\{{}\begin{matrix}2x=54\\3y=108\\z=60\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=27\\y=36\\z=60\end{matrix}\right.\)