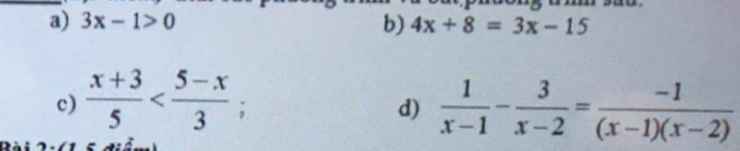a) 3x - 1 > 0
\(\Leftrightarrow\) 3x > 1
\(\Leftrightarrow\) x > \(\dfrac{1}{3}\)
b) 4x + 8 = 3x - 15
\(\Leftrightarrow\) 4x + 8 - 3x + 15 = 0
\(\Leftrightarrow\) x + 23 = 0
\(\Leftrightarrow\) x = -23
Vậy S = \(\left\{-23\right\}\)
c) \(\dfrac{x+3}{5}< \dfrac{5-x}{3}\)
MTC : 15
\(\Rightarrow\dfrac{3\left(x+3\right)}{15}< \dfrac{5\left(5-x\right)}{15}\)
Suy ra : 3(x + 3) < 5(5 - x)
\(\Leftrightarrow\) 3x + 9 < 25 - 5x
\(\Leftrightarrow\) 3x + 5x < 25 - 9
\(\Leftrightarrow\) 8x < 16
\(\Leftrightarrow\) x < \(\dfrac{16}{8}=2\)
d) \(\dfrac{1}{x-1}-\dfrac{3}{x-2}=\dfrac{-1}{\left(x-1\right)\left(x-2\right)}\)
dkxd : x ≠ 1
x ≠ 2
MTC : (x - 1)(x - 2)
Quy đồng mãu thức hai vế của phương trình :
⇒ \(\dfrac{x-2}{\left(x-1\right)\left(x-2\right)}-\dfrac{3\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}\)=\(\dfrac{-1}{\left(x-1\right)\left(x-2\right)}\)
Suy ra : x - 2 - 3(x - 2) = -1
\(\Leftrightarrow\) x - 2 - 3x + 6 + 1 = 0
\(\Leftrightarrow\) -2x + 5 = 0
\(\Leftrightarrow\) -2x = -5
\(\Leftrightarrow\) x = \(\dfrac{-5}{-2}=\dfrac{5}{2}\) (thỏa mãn)
Vậy S = \(\left\{\dfrac{5}{2}\right\}\)
Chúc bạn học tốt