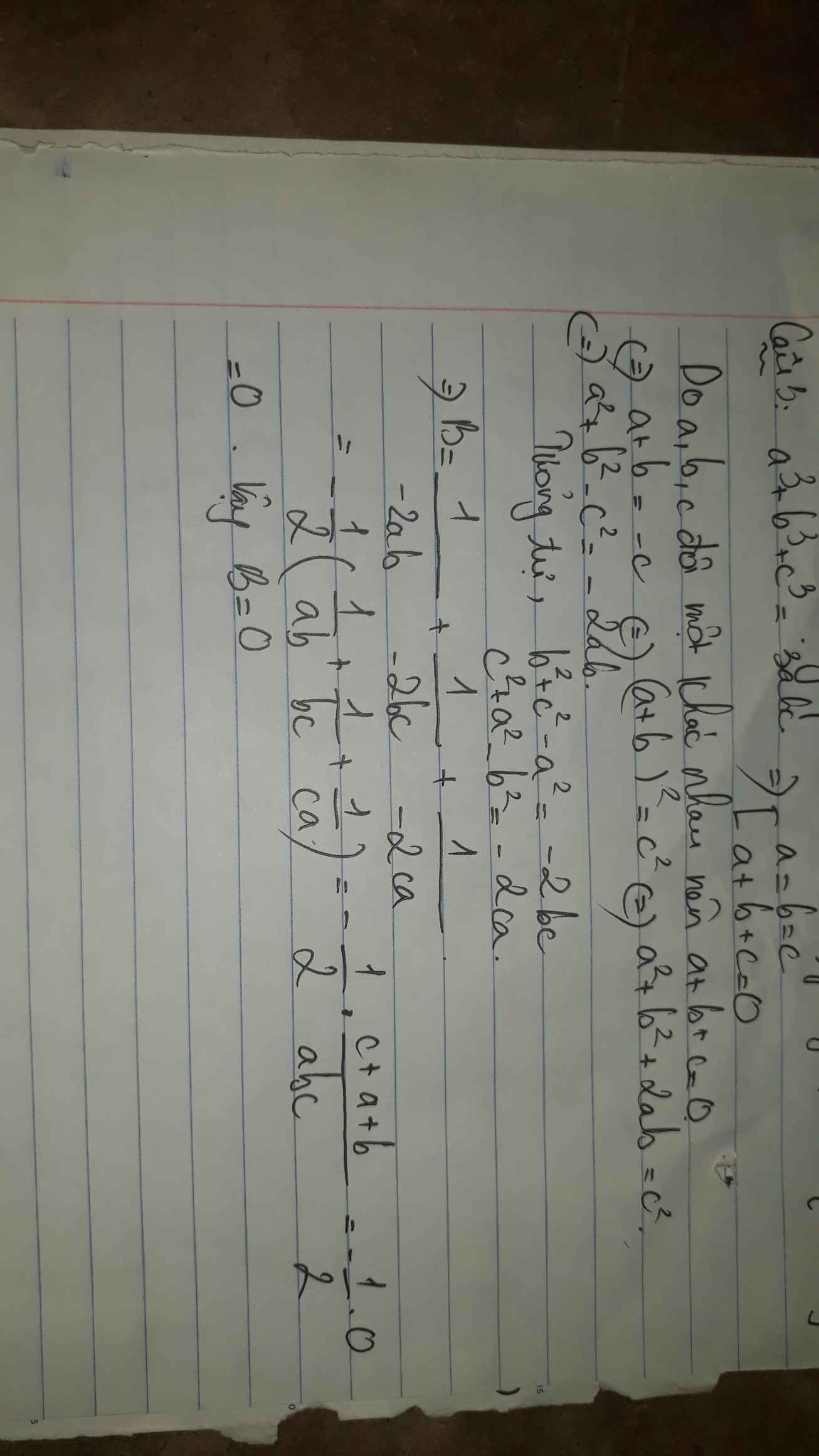1a. Đề lỗi
1b.
\(\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+7+8\right)+15\)
\(=\left(x^2+8x+7\right)^2+8\left(x^2+8x+7\right)+15\)
\(=\left(x^2+8x+7\right)^2+3\left(x^2+8x+7\right)+5\left(x^2+8x+7\right)+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+10\right)+5\left(x^2+8x+10\right)\)
\(=\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)
\(=\left(x^2+8x+10\right)\left(x+2\right)\left(x+6\right)\)
2a.
ĐKXĐ: \(xy\ne0\)
\(\dfrac{2\left(x+y\right)}{xy}=1-\dfrac{1}{xy}\)
\(\Leftrightarrow2\left(x+y\right)=xy-1\)
\(\Leftrightarrow xy-2x-2y-1=0\)
\(\Leftrightarrow x\left(y-2\right)-2\left(y-2\right)-5=0\)
\(\Leftrightarrow\left(x-2\right)\left(y-2\right)=5\)
Phương trình ước số đơn giản, bạn tự lập bảng giá trị
2b.
Gọi 4 số nguyên liên tiếp là \(n;n+1;n+2;n+3\)
Đặt \(S=n^2+\left(n+1\right)^2+\left(n+2\right)^2+\left(n+3\right)^2\)
\(S=4n^2+12n+14=4\left(n^2+3n+3\right)+2\)
Do \(4\left(n^2+3n+3\right)⋮3\) với mọi n nguyên
\(\Rightarrow S\) là 1 số chẵn chia hết cho 2 nhưng ko chia hết cho 4
\(\Rightarrow\) S không thể là SCP (đpcm)
3a.
\(\dfrac{x-1}{2017}+\dfrac{x-2}{2016}+\dfrac{x-3}{2015}+....+\dfrac{x-2016}{2}=2016\)
\(\Leftrightarrow\dfrac{x-1}{2017}-1+\dfrac{x-2}{2016}-1+\dfrac{x-3}{2015}-1+...+\dfrac{x-2016}{2}-1=0\)
\(\Leftrightarrow\dfrac{x-2018}{2017}+\dfrac{x-2018}{2016}+...+\dfrac{x-2018}{2}=0\)
\(\Leftrightarrow\left(x-2018\right)\left(\dfrac{1}{2017}+\dfrac{1}{2016}+...+\dfrac{1}{2}\right)=0\)
\(\Leftrightarrow x-2018=0\) (do \(\dfrac{1}{2017}+\dfrac{1}{2016}+...+\dfrac{1}{2}\ne0\))
\(\Leftrightarrow x=2018\)
3b.
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ac\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(\left(a+b\right)^2-c\left(a+b\right)+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2}{2}\right)=0\)
Do \(a;b;c\) đôi một phân biệt \(\Rightarrow\dfrac{\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2}{2}\ne0\)
\(\Rightarrow a+b+c=0\)
\(\Rightarrow\left\{{}\begin{matrix}c=-\left(a+b\right)\\b=-\left(a+c\right)\\a=-\left(b+c\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c^2=\left(a+b\right)^2\\b^2=\left(a+c\right)^2\\a^2=\left(b+c\right)^2\end{matrix}\right.\)
Nên ta có:
\(B=\dfrac{1}{a^2+b^2-\left(a+b\right)^2}+\dfrac{1}{b^2+c^2-\left(b+c\right)^2}+\dfrac{1}{a^2+c^2-\left(a+c\right)^2}\)
\(\Leftrightarrow B=\dfrac{1}{-2ab}+\dfrac{1}{-2bc}+\dfrac{1}{-2ca}=\dfrac{a+b+c}{-2abc}=\dfrac{0}{-2abc}=0\)
5.
Đặt \(\left(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}\right)=\left(a;b;c\right)\Rightarrow ab+bc+ca=1\)
\(A=\sqrt{\dfrac{bc}{1+a^2}}+\sqrt{\dfrac{ca}{1+b^2}}+\sqrt{\dfrac{ab}{1+c^2}}\)
\(A=\sqrt{\dfrac{bc}{ab+bc+ca+a^2}}+\sqrt{\dfrac{ca}{ab+bc+ca+b^2}}+\sqrt{\dfrac{ab}{ab+bc+ca+c^2}}\)
\(A=\sqrt{\dfrac{bc}{\left(a+b\right)\left(a+c\right)}}+\sqrt{\dfrac{ca}{\left(a+b\right)\left(b+c\right)}}+\sqrt{\dfrac{ab}{\left(a+c\right)\left(b+c\right)}}\)
\(A\le\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{c}{a+c}+\dfrac{c}{b+c}+\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)=\dfrac{3}{2}\) (đpcm)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=\dfrac{1}{\sqrt{3}}\) hay \(x=y=z=\sqrt{3}\)