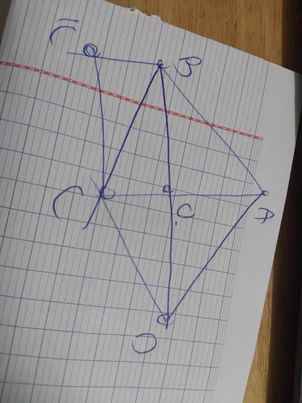
cho tam giác ABC cân tại A.Gọi D,E,F lần lượt là trung điểm của AB,AC,BC 1>lấy K đối xứng với F qua D , chứng minh AFBK À hình chữ nhật 2>Gọi O là dao điểm của EK và AD , H là gia điểm của DF và BE . Chứng minh 1>tứ giác AKDE là hình bình hành 2>HO vuông góc DE
Tứ giác
Hỏi đáp
Bài 1: Tứ giác.
Bài 2: Hình thang
Bài 3: Hình thang cân
Bài 4: Đường trung bình của tam giác, hình thang
Bài 5: Dựng hình bằng thước và compa. Dựng hình thang
Bài 6: Đối xứng trục
Bài 7: Hình bình hành
Bài 8: Đối xứng tâm
Bài 9: Hình chữ nhật
Bài 10: Đường thẳng song song với một đường thẳng cho trước
Bài 11: Hình thoi
Bài 12: Hình vuông
Ôn tập chương I : Tứ giác
1: Xét tứ giác AFBK có
D là trung điểm chung của AB và FK
góc AFB=90 độ
=>AFBK là hình chữ nhật
2: Xét ΔBAC có
BF/BC=BD/BA
nên DF//AC và DF=AC/2
=>DF//AE và DF=AE
=>DK//AE và DK=AE
=>AKDE là hình bình hành
=>AD cắt KE tại trung điểm của mỗi đường
=>O là trung điểm chung của AD và KE
2: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=BC/2
=>DE//BF và DE=BF
=>DEFBlà hình bình hành
=>DF cắt EB tại trung điểm của mỗi đường
=>H là trung điểm chung của FD và EB
Xét ΔEKB có EO/EK=EH/EB
nên OH//KB
=>OH vuông góc BC
=>OH vuông góc DE
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD, kẻ AH, CK vuông góc với BDa/ CM: DHBKb/ CM: tứ giác là hình bình hành.c/ Gọi E là điểm đối xứng với qua . CM : tứ giác là hình thang cân.d/ Gọi P là giao điềm của và . CM : các đường thẳng đồng quy.
Đọc tiếp
Cho hình chữ nhật ABCD, kẻ AH, CK vuông góc với BD
a/ CM: DH=BK
b/ CM: tứ giác là hình bình hành.
c/ Gọi E là điểm đối xứng với qua . CM : tứ giác là hình thang cân.
d/ Gọi P là giao điềm của và .
CM : các đường thẳng đồng quy.
Cho ΔABC cân tại A. Kẻ phân giác trong AM (M ∈ BC). Gọi I là trung điểm của AC và K là điểm đối xứng của M qua I.a)Chứng minh tứgiác AMCK là hình chữ nhật.b)Tính diện tích tam giác ABC, biết AB 5cm; BC 6cm.c)Để tứ giác AMCK là hình vuông thì tam giác ABC phải có them điều kiện gì? cho em hình nữa nhé .-.
Đọc tiếp
Cho ΔABC cân tại A. Kẻ phân giác trong AM (M ∈ BC). Gọi I là trung điểm của AC và K là điểm đối xứng của M qua I.
a)Chứng minh tứgiác AMCK là hình chữ nhật.
b)Tính diện tích tam giác ABC, biết AB = 5cm; BC = 6cm.
c)Để tứ giác AMCK là hình vuông thì tam giác ABC phải có them điều kiện gì?
cho em hình nữa nhé .-.
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
góc AMC=90 độ
Do đó: AMCK là hình chữ nhật
b: BM=CM=BC/2=3cm
\(AM=\sqrt{5^2-3^2}=4\left(cm\right)\)
S=1/2*AM*BC=1/2*6*4=3*4=12cm2
c: Để AMCK là hình vuông thì AM=CM=BC/2
=>ΔABC vuông tại A
Đúng 1
Bình luận (0)
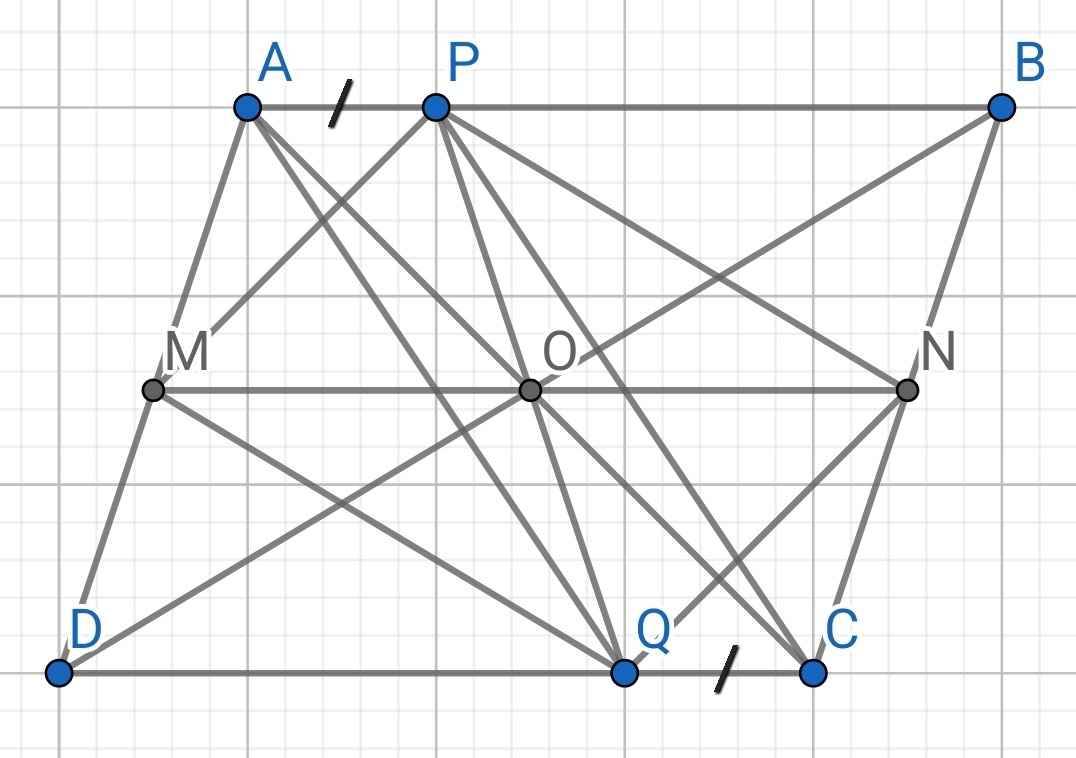
Cho hình bình hành ABCD. Gọi o là giao điểm hai đường thẳng ac và bd. Qua điểm O vẽ đường thẳng song song với AB cắt hai cạnh AD, BC lần lượt tại M, N. Trên AB, CD lần lượt lấy các điểm P, Q sao cho AP = CQ. Chứng minh:
a) Các tứ giác AMNB, APCQ là hình bình hành
b) MP // NQ; MQ = NP
 a) *) Chứng minh AMNB là hình bình hành:
a) *) Chứng minh AMNB là hình bình hành:
Do O là giao điểm của AC và BD
Mà ABCD là hình bình hành (gt)
⇒ O là trung điểm của AC và BD
Do MN // AB (gt)
⇒ OM // CD
∆ACD có
O là trung điểm AC
OM // CD
⇒ M là trung điểm AD
⇒ AM = AD : 2 (1)
Do MN // AB (gt)
⇒ ON // AB
∆ABC có:
O là trung điểm AC (cmt)
ON // AB (cmt)
⇒ N là trung điểm BC
⇒ BN = BC : 2 (2)
Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ AM // BN
Từ (1) và (2) ⇒ AM = BN
Tứ giác AMNB có:
AM // BN (cmt)
AM = BN (cmt)
⇒ AMNB là hình bình hành
*) Chứng minh APCQ là hình bình hành
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AP // CQ
Tứ giác APCQ có:
AP // CQ (cmt)
AP = CQ (gt)
⇒ APCQ là hình bình hành
c) Do O là trung điểm AC (cmt)
M là trung điểm AD (cmt)
⇒ OM là đường trung bình của ∆ACD
⇒ OM = CD : 2 (3)
Do O là trung điểm AC (cmt)
N là trung điểm BC (cmt)
⇒ ON là đường trung bình của ∆ABC
⇒ ON = AB : 2
Mà AB = CD (do ABCD là hình bình hành)
⇒ OM = ON
⇒ O là trung điểm MN
Do APCQ là hình bình hành (cmt)
O là trung điểm AC (cmt)
⇒ O là trung điểm PQ
Tứ giác MPNQ có:
O là trung điểm MN (cmt)
O là trung điểm PQ (cmt)
⇒ MPNQ là hình bình hành
⇒ MP // NQ và MQ = NP
Đúng 2
Bình luận (0)
Bài 5: Cho ∆ABC nhọn ( AB < AC), gọi D và E lần lượt là trung điểm của AB và AC
a) CM: tứ giác BDEC là hình thang
b) Qua D kẻ Dx song song với AC cắt BC tại F, gọi G là trung điểm của DC, CM: 3 điểm
E,G, F thẳng hàng
c) Gọi H là giao điểm của BG và DF, AH cắt GF tại I. CM: H là trọng tâm ABDC và BI //
CD
a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{BC}{2}\)
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Xét tứ giác DECF có
DE//CF
DF//CE
Do đó: DECF là hình bình hành
=>DC cắt EF tại trung điểm của mỗi đường
mà G là trung điểm của DC
nên G là trung điểm của EF
=>E,G,F thẳng hàng
c: Xét ΔABC có
D là trung điểm của BA
DF//AC
Do đó: F là trung điểm của BC
Xét ΔDBC có
DF,BG là các đường trung tuyến
DF cắt BG tại H
Do đó: H là trọng tâm của ΔDBC
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB AC. Gọi E, F lần lượt là trung điểm AB, AC.a) Chứng minh: EF là đường trung bình của tam giác ABC.b) Gọi J là trung điểm BC. Đoạn thẳng AJ cắt đoạn thẳng EF tại S. Chứng minh S là trung điểm EF.c) Kẻ đường cao AH của tam giác ABC. Đoạn thẳng HF và EJ cắt nhau tại I. Chứng minh SI // AH.
Đọc tiếp
Cho tam giác ABC có AB < AC. Gọi E, F lần lượt là trung điểm AB, AC.
a) Chứng minh: EF là đường trung bình của tam giác ABC.
b) Gọi J là trung điểm BC. Đoạn thẳng AJ cắt đoạn thẳng EF tại S. Chứng minh S là trung điểm EF.
c) Kẻ đường cao AH của tam giác ABC. Đoạn thẳng HF và EJ cắt nhau tại I. Chứng minh SI // AH.
a: Xét ΔABC có
E,F lần lượt là trung điểm của AB,AC
=>EF là đường trung bình của ΔABC
b: Xét ΔABC có
E,J lần lượt là trung điểm của BA,BC
=>EJ là đường trung bình của ΔABC
=>EJ//AC và \(EJ=\dfrac{AC}{2}\)
Ta có: EJ//AC
F\(\in\)AC
Do đó: EJ//AF
Ta có: \(EJ=\dfrac{AC}{2}\)
\(AF=\dfrac{AC}{2}\)
Do đó: JE=AF
Xét tứ giác AEJF có
AF//EJ
AF=EJ
Do đó: AEJF là hình bình hành
=>AJ cắt EF tại trung điểm của mỗi đường
=>S là trung điểm chung của AJ và EF
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường trung tuyến AM Gọi D là trung điểm của AB Trên tia đối của tia DM lấy điểm E sao cho DE=DM
Giải thích tại sao tứ giác AEBM là hình thoi
Bài 3: Cho tam giác ABC vuông tại A (AB<AC) có M và E lần lượt là trung điểm của
BC và AC, về MD vuông góc với AB tại a) Chứng minh: MẸ // AB và tứ giác ADME là hình chữ nhật.
b) Gọi K là điểm đối xứng với M qua E. Tứ giác AMCK là hình gì? Chứng minh. c) Gọi O là giao điểm của AM và DE, H là hình chiếu của M trên AK. CM:HD\perp HE
Lời giải:
a. $M,E$ là trung điểm $BC, AC$
$\Rightarrow ME$ là đường trung bình của $ABC$ ứng với $AB$
$\Rightarrow ME\parallel AB$
Mà $AB\perp AC$ nên $ME\perp AC$
$\Rightarrow \widehat{E}=90^0$
Tứ giác $ADME$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên là hcn.
b.
Tứ giác $AMKC$ có 2 đường chéo $AC, MK$ cắt nhau tại trung điểm $E$ của mỗi đường nên là hình bình hành.
Mà $MK\perp AC$ (do $ME\perp AC$)
$\Rightarrow AMKC$ là hình thoi.
c.
Gọi I là giao $DE, HM$
$DM\perp AB, AB\perp AC\Rightarrow DM\parallel AC$
$\Rightarrow \frac{DB}{AD}=\frac{BM}{MC}=1$ (định lý Talet)
$\Rightarrow DB=AD$ hay $D$ là trung điểm $AB$
$ME$ là đường trung bình ứng với cạnh AB
$\Rightarrow ME\parallel AB$ và $ME=\frac{1}{2}AB$
Mà $E$ là trung điểm của $MK$
$\Rightarrow EK\parallel AB$ và $EK=AB:2$
$\Rightarrow EK\parallel DA$ và $EK=DA$
$\Rightarrow DEKA$ là hbh
$\Rightarrow DE\parallel AK$
Mà $HM\perp AK$ nên $DE\perp HM(*)$
Lại có:
$DE\parallel AK \Rightarrow IE\parallel HK$
$\Rightarrow \frac{MI}{IH}=\frac{ME}{EK}=1$
$\Rightarrow MI=IH(**)$
Từ $(*); (**)$ suy ra $DE\perp HM$ tại trung điểm $I$ của $HM$
$\Rightarrow DE$ là đường trung trực của $HM$
$\Rightarrow DH=DM, EH=EM$
$\Rightarrow \triangle DHE=\triangle DME$ (c.c.c)
$\Rightarrow \widehat{DHE}=\widehat{DME}=90^0$
$\Rightarrow DH\perp HE$
Đúng 1
Bình luận (1)
bài này vẽ hình sao v ạ
cho tam giác abc vuông tại a, ab<ac, ah là đuờng cao. Gọi d,e,f là trung điểm của ab,ac,bc. chứng minh de la đuờng trung trực cua ah
ΔHAB vuông tại H
mà HD là trung tuyến
nên HD=AD
ΔHAC vuông tại H
mà HE là trung tuyến
nên EA=EH
EA=EH
DA=DH
=>ED là trung trực của AH
Đúng 1
Bình luận (1)