Bài 7 (2,5 điểm) : Cho ΔABC có AB = AC. Gọi M là trung điểm BC.
a) Chứng minh ΔABM = ΔACM.
b) Trên cạnh AM lấy điểm K bất kỳ. Chứng minh KB = KC.
c) Tia BK cắt cạnh AC tại F, tia CK cắt cạnh AB tại E. Chứng minh EF // CB
Bài 7 (2,5 điểm) : Cho ΔABC có AB = AC. Gọi M là trung điểm BC.
a) Chứng minh ΔABM = ΔACM.
b) Trên cạnh AM lấy điểm K bất kỳ. Chứng minh KB = KC.
c) Tia BK cắt cạnh AC tại F, tia CK cắt cạnh AB tại E. Chứng minh EF // CB
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
=>KM\(\perp\)BC
Xét ΔKBC có
KM là đường cao
KM là đường trung tuyến
Do đó: ΔKBC cân tại K
=>KB=KC
c: Ta có: ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
Ta có: \(\widehat{ABC}=\widehat{ABF}+\widehat{KBC}\)
\(\widehat{ACB}=\widehat{ACE}+\widehat{KCB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
và \(\widehat{KBC}=\widehat{KCB}\)
nên \(\widehat{ABF}=\widehat{ACE}\)
Xét ΔABF và ΔACE có
\(\widehat{ABF}=\widehat{ACE}\)
AB=AC
\(\widehat{BAF}\) chung
Do đó: ΔABF=ΔACE
=>AF=AE
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
vẽ tam giác ABC vuông tại A,C=40độ.Tia phân giác của góc B cắt AC tại D.tính số đo các góc ADC,góc ADB (vẽ hình)
GIÚP MÌNH VỚI Ạ.MÌNH ĐANG CẦN GẤP
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+40^0=90^0\)
=>\(\widehat{ABC}=50^0\)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{DAB}+\widehat{ABD}=45^0+50^0=95^0\)
\(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
=>\(\widehat{ADB}+95^0=180^0\)
=>\(\widehat{ADB}=85^0\)
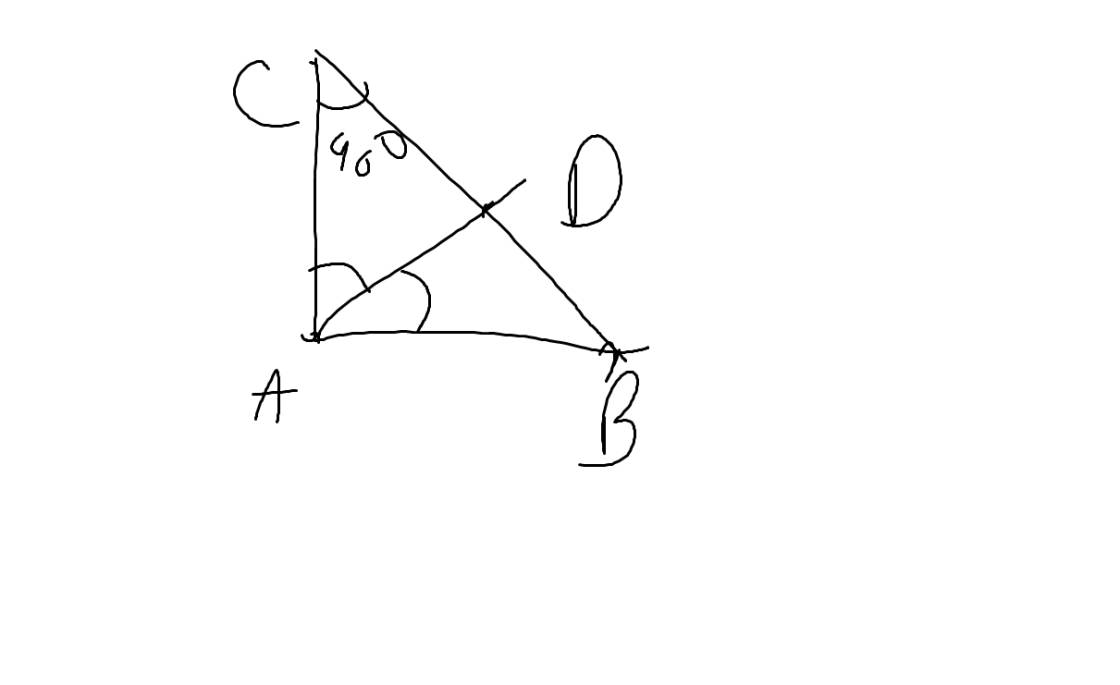
vẽ tam giác ABC vuông góc tại A,B=40độ vẽ AH vuông góc BC(H thuộc BC).Tính số đo góc C,góc BAH,góc CAH
giúp mình với ạ.Mình cần gấp ạ.Mong mọi người giúp đỡ
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}+40^0=90^0\)
=>\(\widehat{ACB}=90^0-40^0=50^0\)
ΔBAH vuông tại H
=>\(\widehat{BAH}+\widehat{B}=90^0\)
=>\(\widehat{BAH}=90^0-40^0=50^0\)
ΔCAH vuông tại H
=>\(\widehat{HAC}+\widehat{C}=90^0\)
=>\(\widehat{HAC}=90^0-\widehat{C}=90^0-50^0=40^0\)
cho tam giác ABC và tam giác MNP
a)Tìm cạnh bằng vạnh AB
b)Nêu tên một cặp góc bằng
Bổ sung đề: Cho tam giác ABC và tam giác MNP bằng nhau
a: ΔABC=ΔMNP
=>AB=MN
b: Một góc bằng góc gì vậy bạn?
Sửa đề: Cho ABC = MNP
a) Do ∆ABC = ∆MNP (gt)
⇒ AB = MN (hai cạnh tương ứng)
b) Một cặp góc bằng nhau:
∠A = ∠M
bài 1 : Cho Δ DEF = Δ MNP . Biết EF + FD = 10cm ,
NP - MP = 2cm, DE = 3cm . Tính các cạnh của mỗi tam giác
bài 2 : Cho 2 tam giác bằng nhau :Δ ABC và 1 tam giác có 3 đỉnh là M,N,P . Hãy viết kí hiệu về sự bằng nhau giữa hai tam giác trong mỗi trường hợp sau , biết :
a) ^A = ^N , ^B = ^M
b) AB= PN, BC= NM
giúp mình với ạ
1:
ΔDEF=ΔMNP
=>DE=MN; EF=NP; DF=MP
EF+FD=10; NP-MP=2; DE=3
=>MN=3cm; EF-DF=2 và EF+FD=10
=>EF=(10+2)/2=6cm và DF=6-2=4cm
EF=NP=6cm; DF=MP=4cm
2:
a: ΔABC=ΔNMP
b: ΔABC=ΔPNM
Bài 1
Do ∆DEF = ∆MNP
⇒ DE = MN; DF = MP; EF = NP
Do NP - MP = 2 (cm)
⇒ EF - FD = 2 (cm)
Lại có
EF + FD = 10 (cm)
⇒ EF = (10 + 2) : 2 = 6 (cm)
⇒ FD = 10 - 6 = 4 (cm)
Vậy độ dài các cạnh của mỗi tam giác là:
EF = NP = 6 cm
FD = MP = 4 cm
DE = MN = 3 cm
Một chiếc kệ sách để bàn gồm các giá đỡ là 9 hình tam giác đều bằng nhau. Biết cạnh tam giác đều là 18cm và khoảng cách giữa mỗi tam giác đều là 2cm. Biết giá một mét nguyên liệu là 50 000 đồng. Em hãy tính tiền nguyên liệu phải trả khi thiết kế chiếc giá đỡ trên
Đầu tiên, ta cần tính diện tích một tam giác đều:Diện tích tam giác đều = (cạnh)^2 * sqrt(3) / 4Diện tích tam giác đều = (18)^2 * sqrt(3) / 4Diện tích tam giác đều = 81 * sqrt(3) cm^2Tiếp theo, ta tính diện tích của tất cả 9 tam giác đều trên chiếc kệ sách:Diện tích của 9 tam giác đều = 81 * sqrt(3) cm^2 * 9Diện tích của 9 tam giác đều = 729 * sqrt(3) cm^2Tiếp theo, ta tính diện tích nguyên chiếc kệ sách:Diện tích nguyên chiếc kệ sách = (cạnh tam giác + khoảng cách) * (khoảng cách + chiều cao tam giác)Diện tích nguyên chiếc kệ sách = (18 cm + 2 cm) * (2 cm + 18 cm)Diện tích nguyên chiếc kệ sách = 20 cm
Xét ΔAMC và ΔANC ta có:
\(\widehat{MAC}=\widehat{ANC}\left(gt\right)\)
\(\widehat{MCA}=\widehat{NCA}\left(gt\right)\)
\(AC\) là cạnh chung
\(\Rightarrow\) ΔAMC = ΔANC (g-c-g)
Từ đó ta có:
AM = AN (hai cạnh tương ứng)
........................... =) AMC = ANC
........................... =) AM = AN
Một chiếc kệ sách để bàn gồm các giá đỡ là 9 hình tam giác đều bằng nhau. Biết cạnh tam giác đều là 18cm và khoảng cách giữa mỗi tam giác đều là 2cm. Biết giá một mét nguyên liệu là 50 000 đồng. Em hãy tính tiền nguyên liệu phải trả khi thiết kế chiếc giá đỡ trên
* Cách 1
∆ADE có AD = AE (gt)
⇒ ∆ADE cân tại A
⇒ ∠ADE = ∠AED (hai góc ở đáy)
* Cách 2
Xét ∆ABD và ∆ACE có:
AB = AC (gt)
AD = AE (gt)
BD = CE (gt)
⇒ ∆ABD = ∆ACE (c-c-c)
∠ADB = ∠AEC
Mà ∠ADB + ∠ADE = 180⁰ (kề bù)
∠AEC + ∠AED = 180⁰ (kề bù)
⇒ ∠ADE = ∠AED
cho tam giác abc vuông tại a M là điểm trên cạnh AB VẼ MN vuông góc với BC tại N gọi K là giao điểm của AC và MN chứng minh a> BAH= B > x AH và B bù nhau