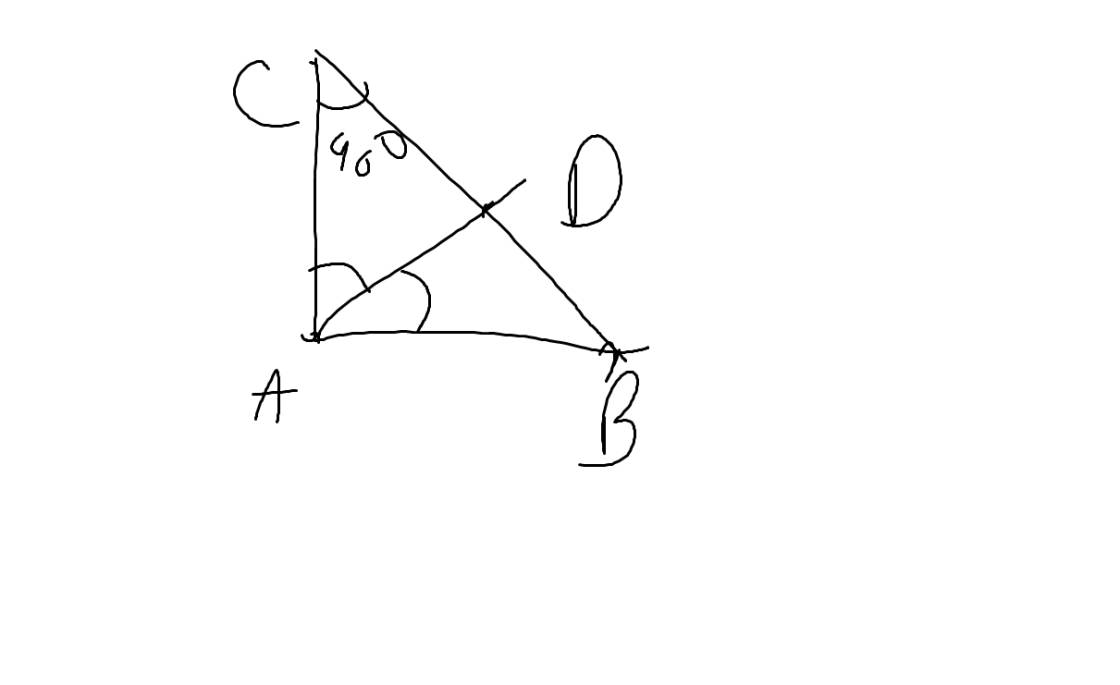
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+40^0=90^0\)
=>\(\widehat{ABC}=50^0\)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{DAB}+\widehat{ABD}=45^0+50^0=95^0\)
\(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
=>\(\widehat{ADB}+95^0=180^0\)
=>\(\widehat{ADB}=85^0\)