Em hãy nêu các hoạt động thể giữ gìn và phát huy truyền thống ngày Tết?
Xem chi tiết
Mỗi khoảng thời gian ứng với những hoạt động như: Đưa ông Táo về trời vào ngày 23 tháng Chạp; Gói bánh chưng, bánh tét; Chưng hoa ngày tết như hoa đào , mai ,quất ...
Đúng 0
Bình luận (0)
các hoạt động giữ gìn và phất huy ngày tết là:
- dọn dẹp nhà cửa và trang trí nhà của cho có không gian tết âm cúng vui vè hơn
- gói bánh chưng bánh tét với gia đình họ hàng
- hỏi tham chúc tết
- lì xì và nhận lì xì
- mặc áo dài truyền thống dân tộc( đồ nữ)
Đúng 4
Bình luận (0)
Để giữ gìn và phát huy truyền thống ngày Tết, chúng ta có thể thực hiện nhiều hoạt động ý nghĩa:
- Trước tiên, việc dọn dẹp, trang trí nhà cửa và bày mâm ngũ quả không chỉ làm cho không gian sống thêm tươi mới mà còn thể hiện lòng hiếu kính với tổ tiên
- Chúng ta nên duy trì tục lệ thăm hỏi, chúc Tết ông bà, cha mẹ và họ hàng để thắt chặt tình cảm gia đình
-Các trò chơi dân gian, lễ hội truyền thống hay múa lân cũng là những nét đẹp văn hóa cần được bảo tồn
-Ngoài ra, việc gói bánh chưng, bánh tét, hoặc chuẩn bị các món ăn ngày Tết giúp gắn kết các thành viên trong gia đình và lưu giữ tinh hoa ẩm thực Việt
-Chúng ta cần giáo dục thế hệ trẻ về ý nghĩa của ngày Tết thông qua những câu chuyện cổ tích, tục ngữ, và lễ nghi để những giá trị truyền thống được truyền lại qua nhiều thế hệ
.......
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
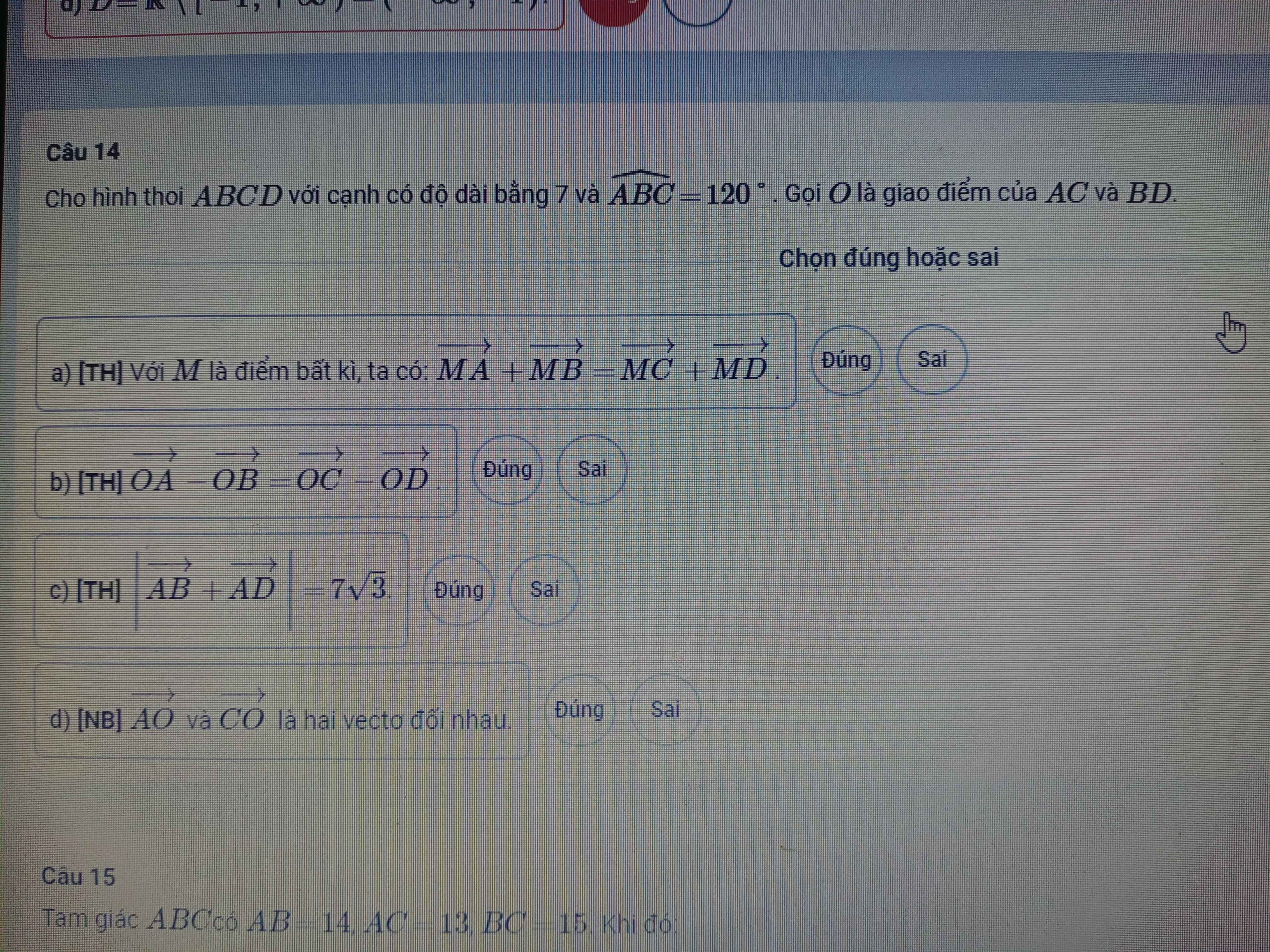giúp em với
a) \(O\) là trọng tâm hình thoi \(ABCD\) (tính chất hình thoi)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=4\overrightarrow{MO}-\left(\overrightarrow{MC}+\overrightarrow{MD}\right)\)
\(\Rightarrow\) Sai
b) \(\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{DC}\left(vô.lý\right)\)
\(\Rightarrow\) Sai
c) \(\left(\widehat{\overrightarrow{AB};\overrightarrow{AD}}\right)=\widehat{BAD}=\dfrac{360^o-2.120^o}{2}=60^o\)
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=AB^2+AD^2+2.AB.AD.cos\left(\widehat{\overrightarrow{AB};\overrightarrow{AD}}\right)\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=2AB^2+2AB^2.cos60^o\left(AB=AD\right)\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=2AB^2+2AB^2.\dfrac{1}{2}=3AB^2\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AB\sqrt{3}=7\sqrt{3}\)
\(\Rightarrow\) Đúng
d) Đúng (\(O\) là trung điểm \(AC\) - tính chất hình thoi)
Đúng 1
Bình luận (0)
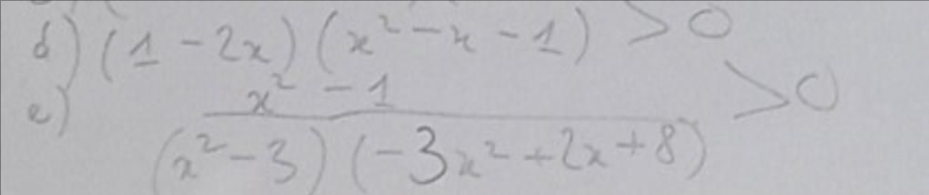
Giải BPT, lập bảng xét dấu giúp em với ạ
d, $1-2x=0\Leftrightarrow x=\dfrac{1}{2}$
$x^2-x-1=0\Leftrightarrow x=\dfrac{1\pm\sqrt 5}{2}$
Bảng xét dấu:
\begin{array}{|c|cc|}\hline x&-\infty&&\dfrac{1-\sqrt 5}{2}&&\dfrac{1}{2}&&\dfrac{1+\sqrt 5}{2}&&+\infty\\\hline 1-2x&&+&|&+&0&-&|&-&\\\hline x^2-x-1&&+&0&-&|&-&0&+&\\\hline f(x)&&+&0&-&0&+&0&-&\\\hline\end{array}
$f(x)>0\Rightarrow x\in\left(-\infty;\dfrac{1-\sqrt 5}{2}\right)\cup\left(\dfrac{1}{2};\dfrac{1+\sqrt 5}{2}\right)$
Vậy $ x\in\left(-\infty;\dfrac{1-\sqrt 5}{2}\right)\cup\left(\dfrac{1}{2};\dfrac{1+\sqrt 5}{2}\right)$
e, $x^2-1=0\Leftrightarrow x=\pm 1$
$x^2-3=0\Leftrightarrow x=\pm\sqrt 3$
$-3x^2+2x+8=0\Leftrightarrow \left[\begin{array}{1}x=2\\x=-\dfrac{4}{3}\end{array}\right.$
Bảng xét dấu:
$\begin{array}{|c|cc|}\hline x&-\infty&&-\sqrt 3&&-\dfrac{4}{3}&&-1&&1&&\sqrt 3&&2&&+\infty\\\hline x^2-1&&+&|&+&|&+&0&-&0&+&|&+&|&+&\\\hline x^2-3&&+&0&-&|&-&|&-&|&-&0&+&|&+&\\\hline -3x^2+2x+8&&-&|&-&0&+&|&+&|&+&|&+&0&-&\\\hline f(x)&&-&||&+&||&-&0&+&0&-&||&+&||&-&\\\hline\end{array}$
$f(x)>0\Rightarrow x\in\left(-\sqrt 3;-\dfrac{4}{3}\right)\cup (-1;1)\cup (\sqrt 3;2)$
Vậy $x\in\left(-\sqrt 3;-\dfrac{4}{3}\right)\cup (-1;1)\cup (\sqrt 3;2)$
Đúng 1
Bình luận (0)
14 tháng 12 2024 lúc 17:03
giúp vớiiii
Xét tam giác vuông \(IAB:\)
\(IB^2=IA^2+AB^2=\left(\dfrac{3a}{2}\right)^2+16a^2=\dfrac{73a^2}{4}\)
\(\Rightarrow IB=\dfrac{a\sqrt{73}}{2}\)
\(tan\widehat{AIB}=\dfrac{AB}{IA}=\dfrac{4a}{\dfrac{3a}{2}}=\dfrac{8}{3}\)
\(\Rightarrow tan\widehat{DIB}=tan\left(180^o-\widehat{AIB}\right)=-tan\widehat{AIB}=-\dfrac{8}{3}\)
\(1+tan^2\widehat{DIB}=\dfrac{1}{cos^2\widehat{DIB}}\)
\(\Rightarrow cos^2\widehat{DIB}=\dfrac{1}{1+tan^2\widehat{DIB}}=\dfrac{1}{1+\dfrac{64}{9}}=\dfrac{9}{73}\)
\(\Rightarrow cos\widehat{DIB}=-\dfrac{3}{\sqrt{73}}\) (\(\widehat{DIB}\) thuộc góc phần tư số \(II\))
\(\Rightarrow cos\left(\widehat{\overrightarrow{IB};\overrightarrow{ID}}\right)=cos\widehat{DIB}=-\dfrac{3}{\sqrt{73}}\)
\(\left(\overrightarrow{IA}+\overrightarrow{IB}\right).\overrightarrow{ID}=\overrightarrow{IA}.\overrightarrow{ID}+\overrightarrow{IB}.\overrightarrow{ID}\)
\(=IA.ID.cos180^o+IB.ID.cos\left(\widehat{\overrightarrow{IB};\overrightarrow{ID}}\right)\)
\(=\dfrac{3a}{2}.\dfrac{3a}{2}.\left(-1\right)+\dfrac{a\sqrt{73}}{2}.\dfrac{3a}{2}.\left(-\dfrac{3}{\sqrt{73}}\right)\)
\(=-\dfrac{9a^2}{4}-\dfrac{9a^2}{4}=-\dfrac{9a^2}{2}\)
Đúng 1
Bình luận (0)
13 tháng 12 2024 lúc 17:09
Giúp em bài này với ạ, nghĩ hoài không ra 🥲
Cho tam giác ABC , có N là trung điểm BC , K là trung điểm AN . Chứng minh vecto 2NA+NB+NC=0
12 tháng 12 2024 lúc 20:47
Giúp tớ bài này với,cần gấp,vẽ hình rồi chi tiết ra nhé !Anh Quang dự định mua một chiếc xe tải chiều rộng là 2,4m làm dịch vụ vận chuyển hàng hoá cho nhân dân trong xã .Vì đường vào xã có cổng hình parabol (hưỡng về lõm xuống dưới), khoảng cách giữa hai chân cổng là 4,2m và khoảng cách từ đỉnh cổng đến mặt đất là 4,41m .Để xe tải anh Quang dự định mua có thể đi qua cổng thì chiều cao tối đa của xe là bao nhiêu ?
Đọc tiếp
Giúp tớ bài này với,cần gấp,vẽ hình rồi chi tiết ra nhé !
Anh Quang dự định mua một chiếc xe tải chiều rộng là 2,4m làm dịch vụ vận chuyển hàng hoá cho nhân dân trong xã .Vì đường vào xã có cổng hình parabol (hưỡng về lõm xuống dưới), khoảng cách giữa hai chân cổng là 4,2m và khoảng cách từ đỉnh cổng đến mặt đất là 4,41m .Để xe tải anh Quang dự định mua có thể đi qua cổng thì chiều cao tối đa của xe là bao nhiêu ?
Chọn gốc tọa độ \(O\left(0;0\right)\) tại đỉnh Parabol, \(\overrightarrow{Ox}\) hướng từ trái sang phải; \(\overrightarrow{Oy}\) hướng từ dưới lên trên
Đồ thị Parabol có dạng \(y=ax^2\left(P\right)\)
Tọa độ chân cổng \(\left(2,1;-4,41\right)\in\left(P\right)\Leftrightarrow-4,41=a.2,1^2\Leftrightarrow a=-1\)
\(\Rightarrow y=-x^2\)
Chiều rộng xe tải là \(2,4\left(m\right)\)
\(\Rightarrow\) Hoành độ 2 bánh xe là \(x=\pm\dfrac{2,4}{2}=\pm1,2\)
\(\Rightarrow\) Tung độ của xe 2 bánh xe chính là chiều cao tối đa của xe
\(\left|y\right|=\left|-1,2^2\right|=1,44\left(m\right)\)
Vậy anh Quang dự định mua xe tải có chiều cao tối đa để qua cổng là \(1,44\left(m\right)\)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD. Gọi I, J tương ứng là trung điểm của các cạnh AB, CD.a) Chứng minh rằng BC+AD=2IJ = AC+BD.
Xem chi tiết
b) Hãy xác định điểm M để MA+3MB+2MC=0.
c) Cho AB = c, AC = b và BC = a. Tính AB.AC theo a, b, c.
11 tháng 12 2024 lúc 20:24
GIÚP VỚIIII
Ta có \(h\left(x\right)=0\) thì quả bóng chạm đất, độ cao \(h=0\)
\(\Rightarrow-0,0083x^2+0,1x+3,1=0\)
\(\Delta=0,1^2+4.3,1.0,0083=0,11292\)
\(\Rightarrow\sqrt{\Delta}\approx0,34\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{-0,1+0,34}{2.\left(-0,0083\right)}=-14,46\left(ktm\right)\\x=\dfrac{-0,1-0,34}{2.\left(-0,0083\right)}=26,51\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow\) khoảng cách từ vị trí đặt trái bóng đến vạch vôi khung thành là \(26,51\left(m\right)\)
Đúng 1
Bình luận (0)
cho hình vuông ABCD. Điểm M nằm trên đoạn thẳng AC sao cho AM=AC/4. Gọi N là trung điểm CD. Chứng minh tam giác BMN là tam giác vuông cân