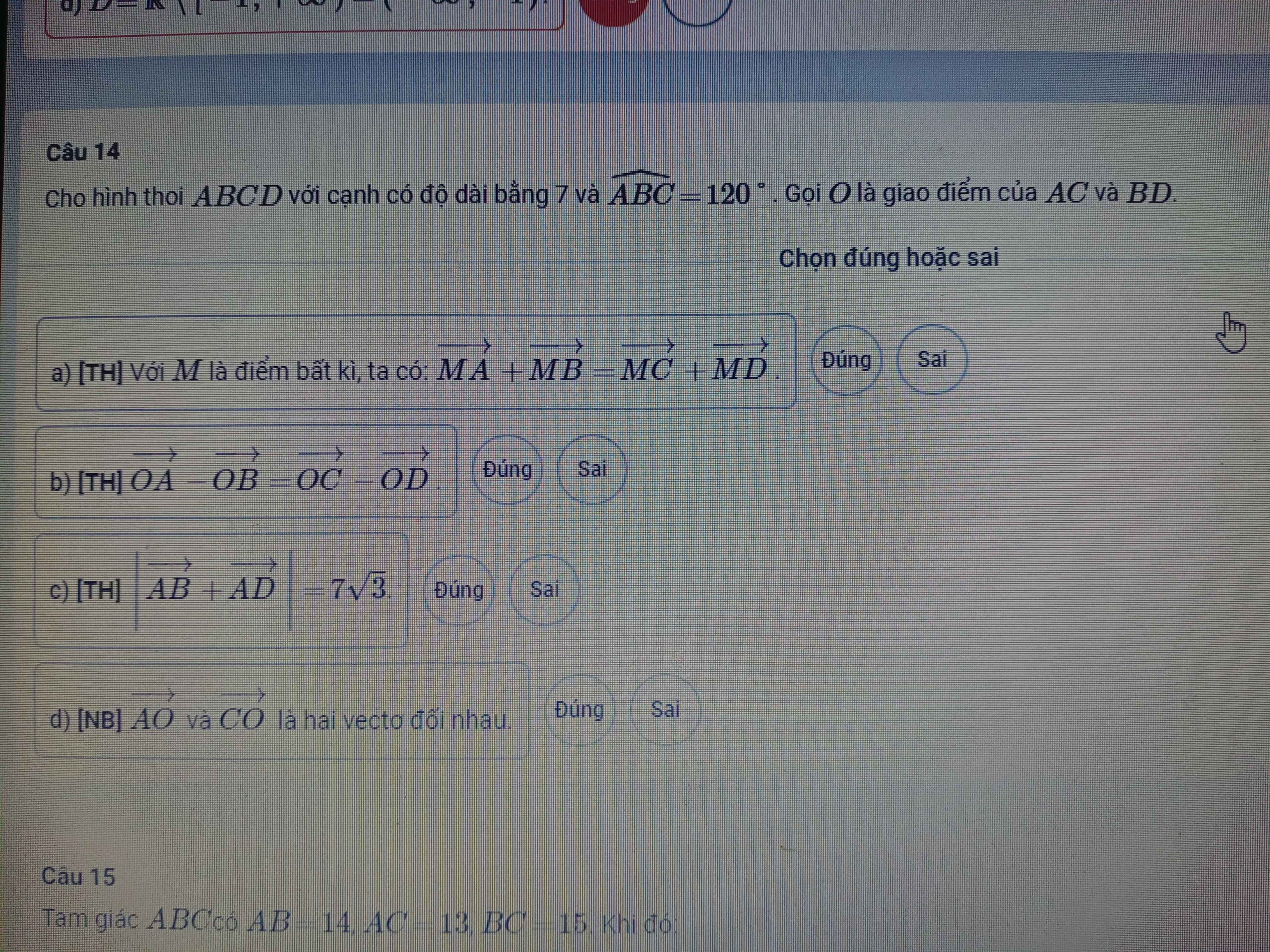
a) \(O\) là trọng tâm hình thoi \(ABCD\) (tính chất hình thoi)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=4\overrightarrow{MO}-\left(\overrightarrow{MC}+\overrightarrow{MD}\right)\)
\(\Rightarrow\) Sai
b) \(\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{DC}\left(vô.lý\right)\)
\(\Rightarrow\) Sai
c) \(\left(\widehat{\overrightarrow{AB};\overrightarrow{AD}}\right)=\widehat{BAD}=\dfrac{360^o-2.120^o}{2}=60^o\)
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=AB^2+AD^2+2.AB.AD.cos\left(\widehat{\overrightarrow{AB};\overrightarrow{AD}}\right)\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=2AB^2+2AB^2.cos60^o\left(AB=AD\right)\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|^2=2AB^2+2AB^2.\dfrac{1}{2}=3AB^2\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AB\sqrt{3}=7\sqrt{3}\)
\(\Rightarrow\) Đúng
d) Đúng (\(O\) là trung điểm \(AC\) - tính chất hình thoi)