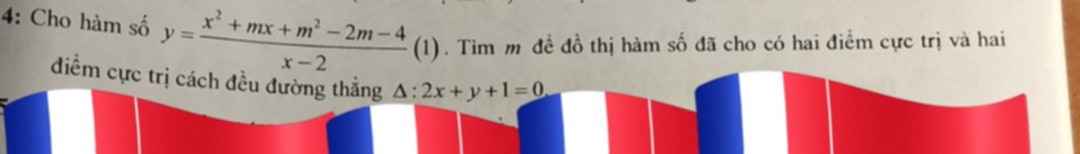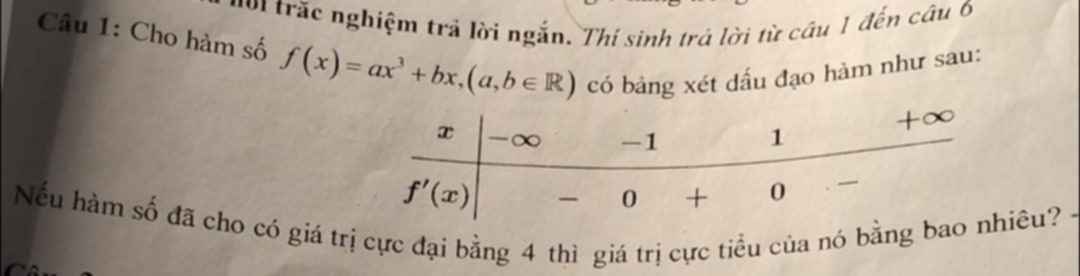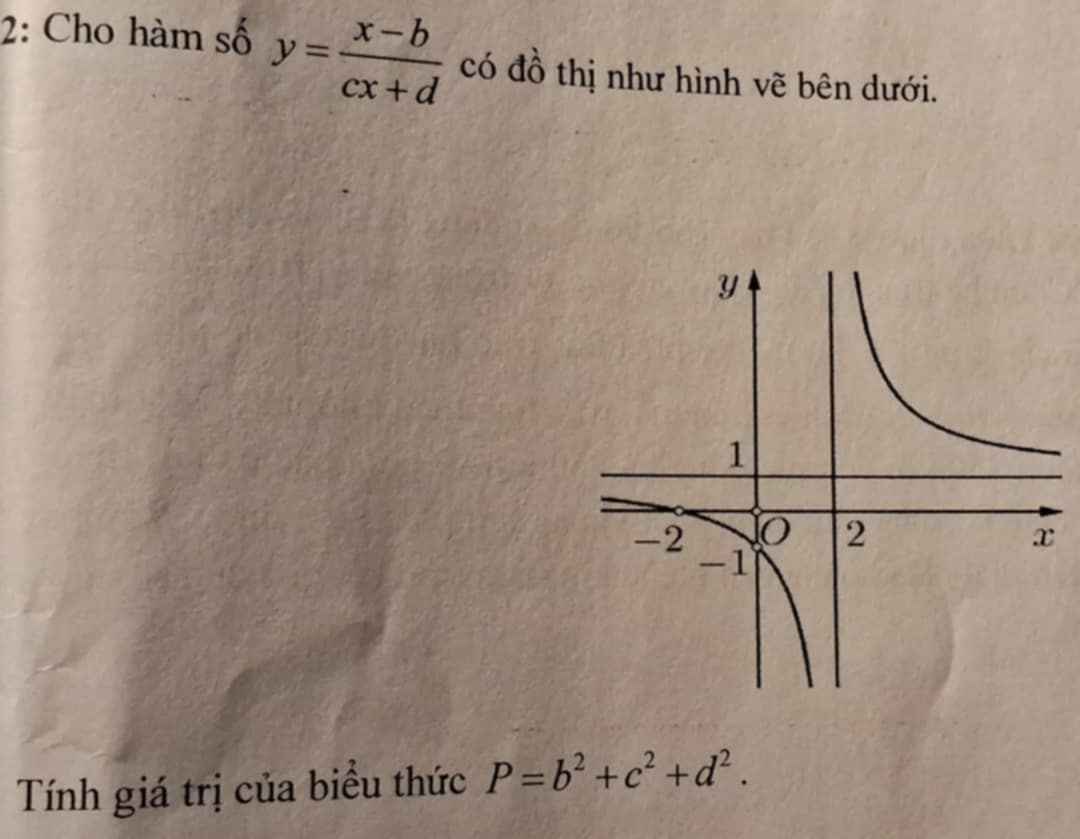
\(TCĐ:x=2\Leftrightarrow-\dfrac{d}{c}=2\Leftrightarrow d=-2c\)
\(TCN:y=1\Leftrightarrow\dfrac{1}{c}=1\Leftrightarrow c=1\Rightarrow d=-2\)
\(\Rightarrow y=\dfrac{x-b}{x-2}\left(C\right)\)
\(\left(-2;0\right)\in\left(C\right)\Leftrightarrow0=\dfrac{-2-b}{-2-2}\Leftrightarrow b=-2\)
\(\Rightarrow y=\dfrac{x+2}{x-2}\left(C\right)\)
Kiểm tra \(\left(0;-1\right)\in\left(C\right)\Leftrightarrow\dfrac{0+2}{0-2}=-1\left(đúng\right)\)
\(P=b^2+c^2+d^2=\left(-2\right)^2+1^2+\left(-2\right)^2=9\)
Đúng 0
Bình luận (0)
Cho hình lập phương abcd.a'b'c'd' có cạnh bằng a.Trên các cạnh AA',CC' lần lượt lấy các điểm M,N sao cho AM=2/3AA',CN=NC'
Tính vecto AN.vecto A'C'=?
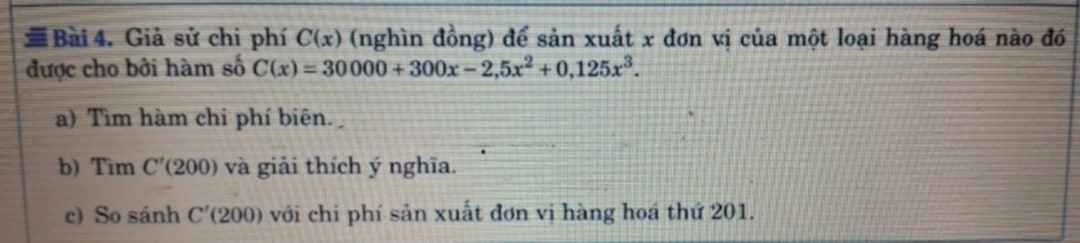
a) Hàm chi phí biên là: \(C'\left(x\right)=300-5x+0,375x^2\left(nghìn.đồng/đơn.vị\right)\)
b) \(C'\left(200\right)=300.200-5.200^2+0,375.200^3=14300\)
Ý nghĩa : khi sản xuất thêm một đơn vị hàng hóa thứ \(201\), chi phí sản xuất sẽ tăng thêm khoảng \(14300\left(nghìn.đồng\right)\) hay chi phí để sản xuất đơn vị hàng hóa thứ \(201\) ước tính là \(14300\left(nghìn.đồng\right)\)
c) \(C'\left(x\right)=300-5x+0,375x^2>0,\forall x>0\)
\(\Rightarrow C'\left(x\right)\) có đồ thị là 1 Parabol đạt cực tiểu tại \(x=\dfrac{5}{2.0,375}\approx6,67\) \(\Rightarrow C'\left(x\right)\) tăng trên \(D=\left(6,67;+\infty\right)\)
\(\Rightarrow C'\left(201\right)>C'\left(200\right)\)
Đúng 1
Bình luận (0)
\(f'\left(x\right)=3ax^2+b\)
\(f'\left(-1\right)=f\left(1\right)=0\Leftrightarrow3a+b=0\left(1\right)\)
Theo Bảng biến thiên ta được \(a< 0\) \(\left(f'\left(x\right)>0,x\in\left(-1;1\right)\right)\)
\(f\left(x\right)_{max}=4\) tại \(x=1\)
\(\Rightarrow a.1^3+b=4\Leftrightarrow a+b=4\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}3a+b=0\\a+b=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-2< 0\left(tm\right)\\b=6\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=-2x^3+6x\)
\(\Rightarrow f\left(-1\right)_{min}=-2.\left(-1\right)^3+6.\left(-1\right)=-4\)
Vậy HS đạt cực tiểu tại \(x=-1\) có giá trị là \(-4\)
Đúng 1
Bình luận (0)
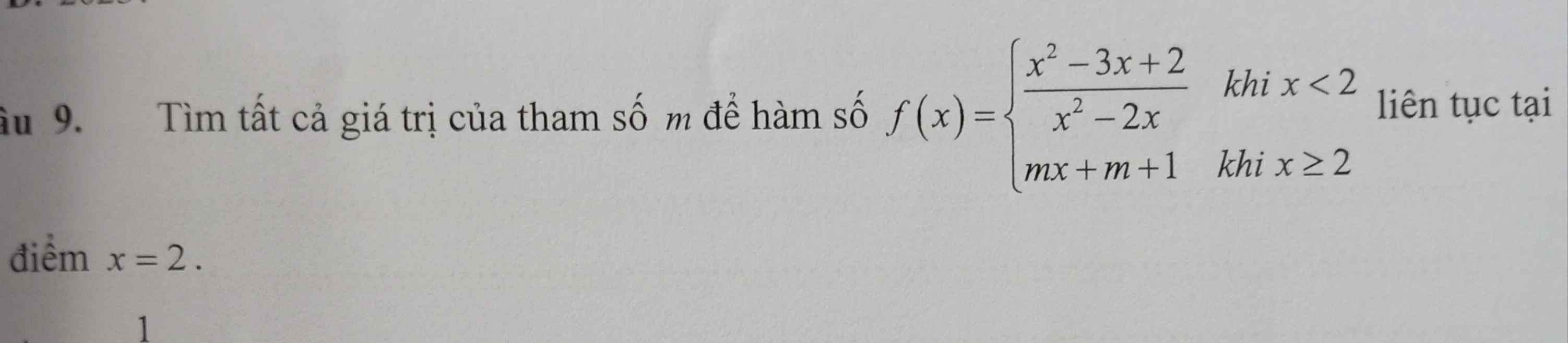 mng giúp em bài này với ạ
mng giúp em bài này với ạ
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x^2-3x+2}{x^2-2x}\)
\(=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{x\cdot\left(x-2\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x}=\dfrac{2-1}{2}=\dfrac{1}{2}\)
\(f\left(2\right)=m\cdot2+m+1=3m+1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=m\cdot2+m+1=3m+1\)
Để f(x) liên tục tại x=2 thì \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}\)
=>\(3m+1=\dfrac{1}{2}\)
=>\(3m=-\dfrac{1}{2}\)
=>\(m=-\dfrac{1}{6}\)
Đúng 1
Bình luận (0)