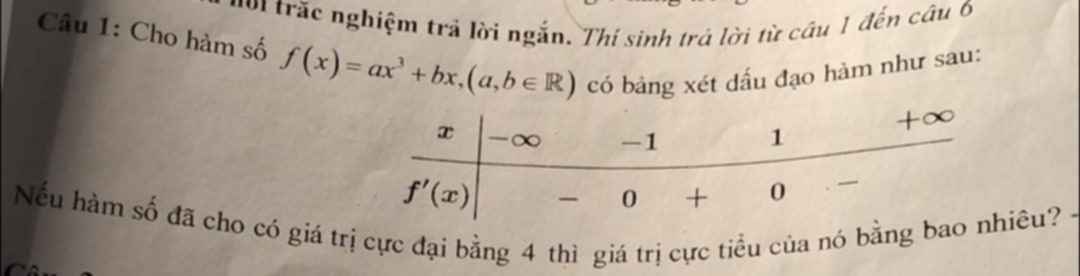\(f'\left(x\right)=3ax^2+b\)
\(f'\left(-1\right)=f\left(1\right)=0\Leftrightarrow3a+b=0\left(1\right)\)
Theo Bảng biến thiên ta được \(a< 0\) \(\left(f'\left(x\right)>0,x\in\left(-1;1\right)\right)\)
\(f\left(x\right)_{max}=4\) tại \(x=1\)
\(\Rightarrow a.1^3+b=4\Leftrightarrow a+b=4\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}3a+b=0\\a+b=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-2< 0\left(tm\right)\\b=6\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=-2x^3+6x\)
\(\Rightarrow f\left(-1\right)_{min}=-2.\left(-1\right)^3+6.\left(-1\right)=-4\)
Vậy HS đạt cực tiểu tại \(x=-1\) có giá trị là \(-4\)