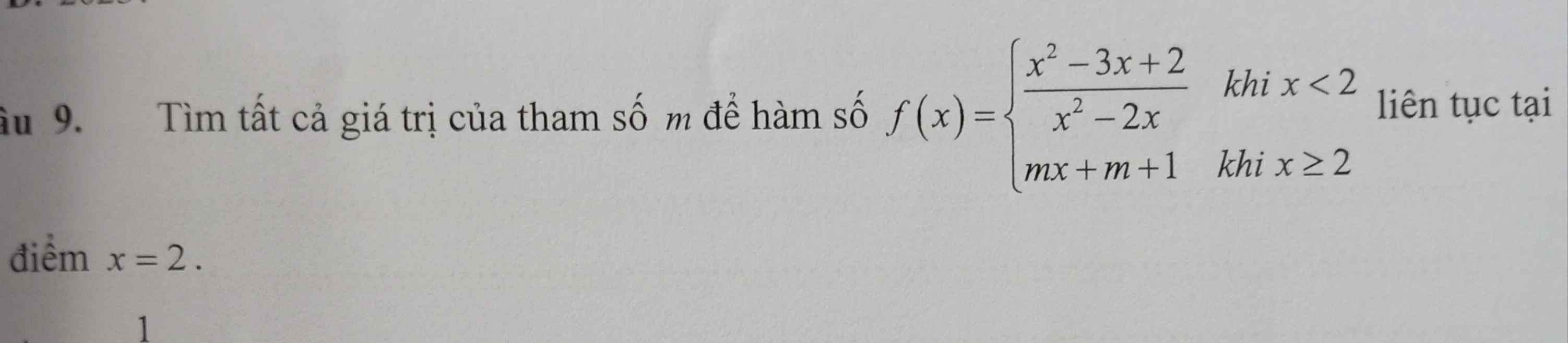\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x^2-3x+2}{x^2-2x}\)
\(=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{x\cdot\left(x-2\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x}=\dfrac{2-1}{2}=\dfrac{1}{2}\)
\(f\left(2\right)=m\cdot2+m+1=3m+1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=m\cdot2+m+1=3m+1\)
Để f(x) liên tục tại x=2 thì \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}\)
=>\(3m+1=\dfrac{1}{2}\)
=>\(3m=-\dfrac{1}{2}\)
=>\(m=-\dfrac{1}{6}\)
Đúng 1
Bình luận (0)
