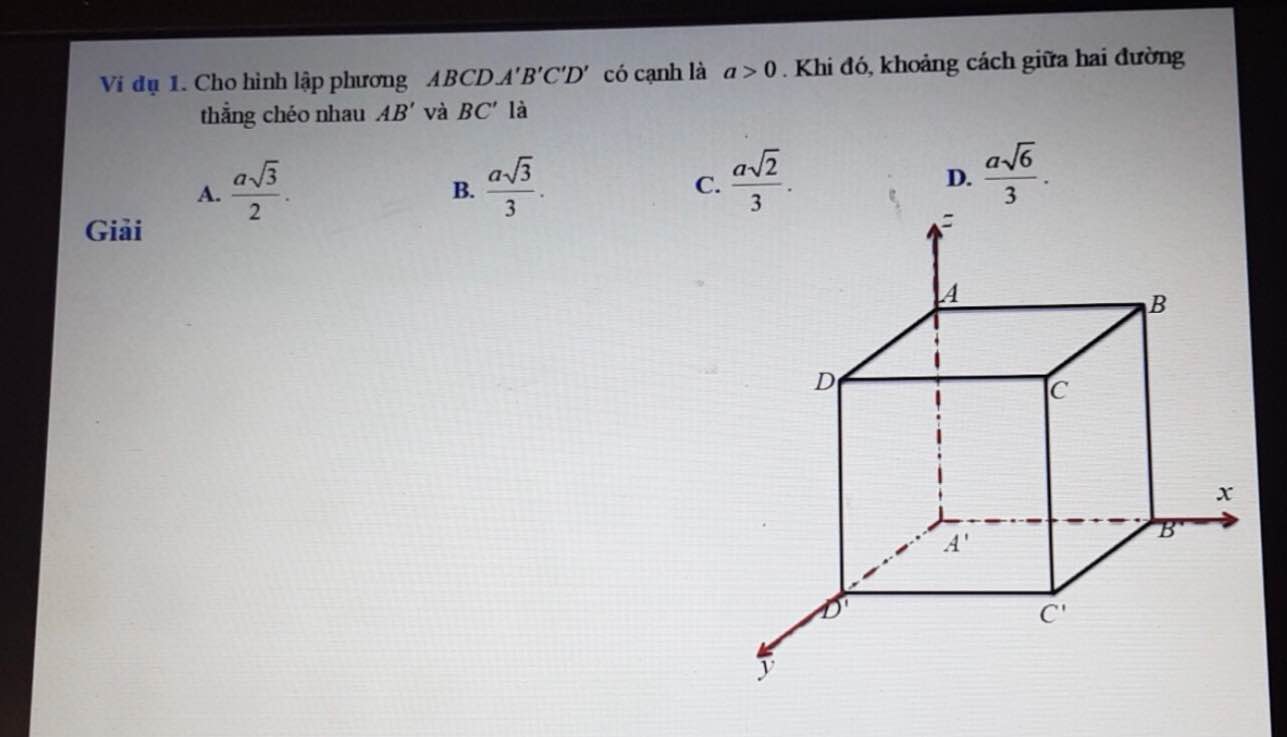
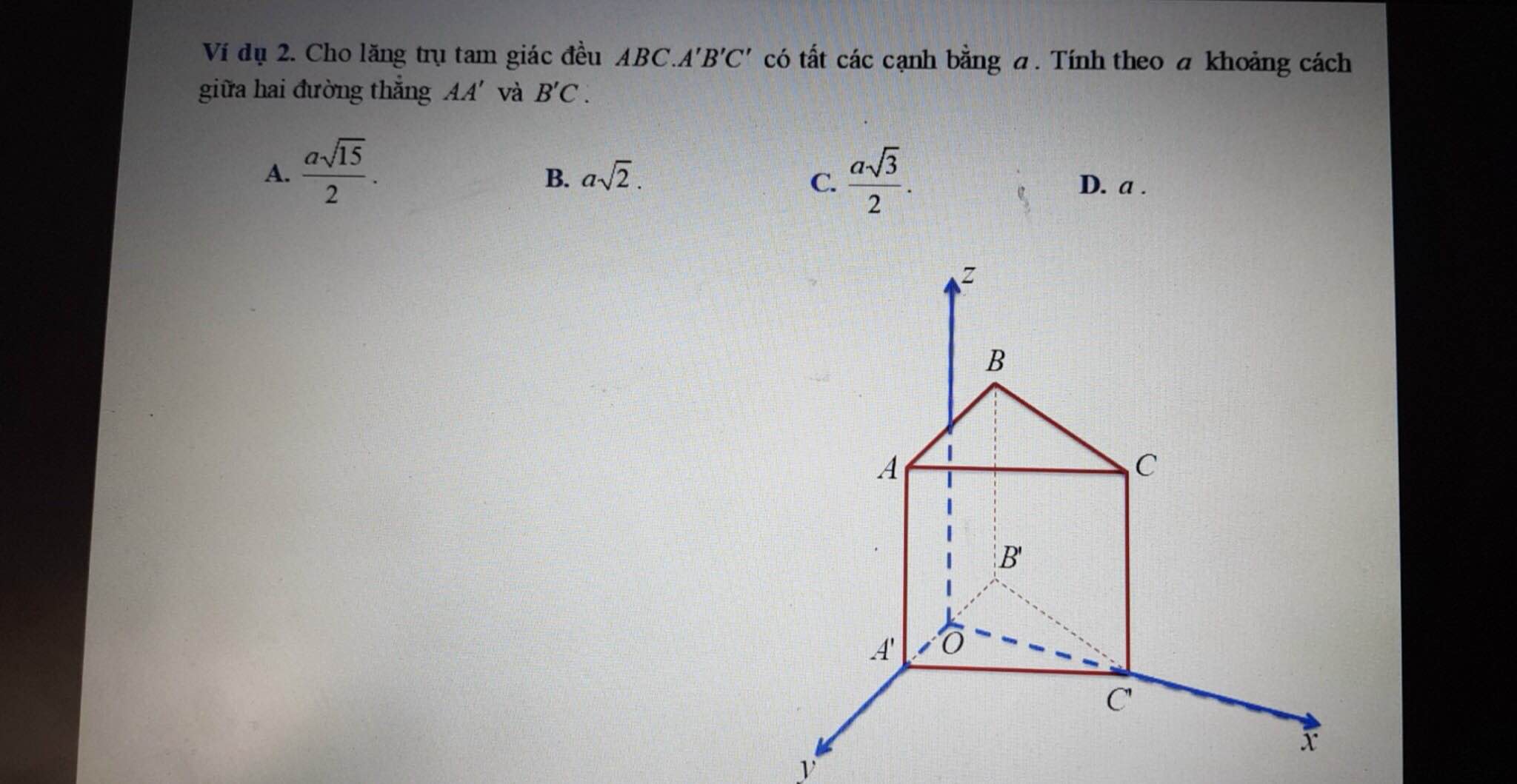
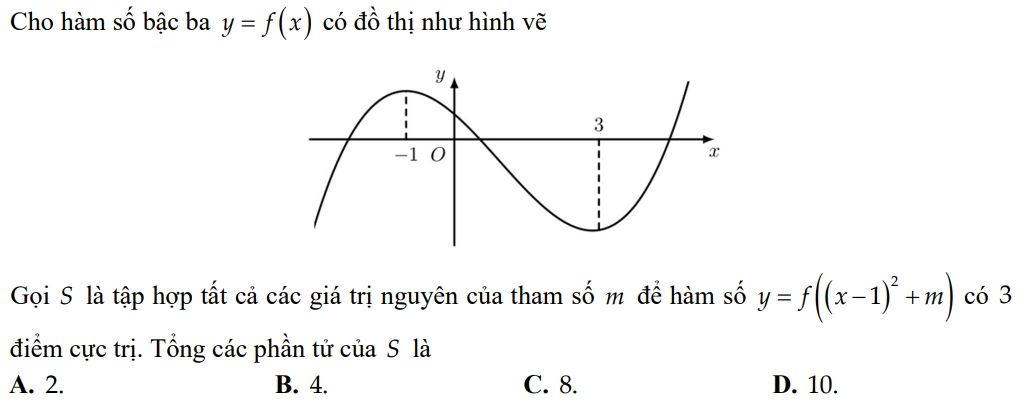
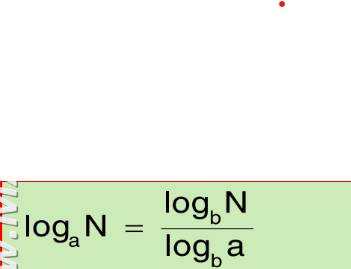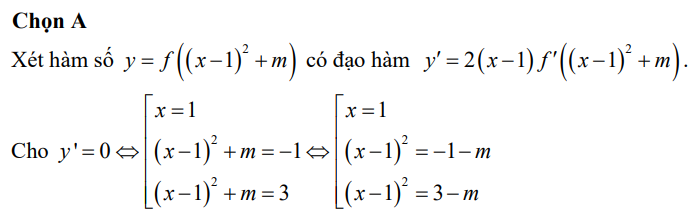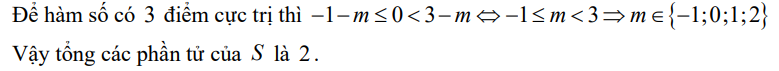Nhìn hình minh họa thì rõ ràng họ hướng ngay đến cách giải sử dụng tọa độ hóa nên chúng ta đi theo hướng đó:
Đặt hệ trục tọa độ Oxyz vào lập phương như hình vẽ và quy ước a bằng 1 đơn vị độ dài
Ta có các tọa độ điểm: \(A\left(0;0;1\right)\) ; \(B\left(1;0;1\right)\); \(B'\left(1;0;0\right)\); \(C'\left(1;1;0\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(1;0;-1\right)\); \(\overrightarrow{BC'}=\left(0;1;-1\right)\) ; \(\overrightarrow{AB}=\left(1;0;0\right)\)
\(\Rightarrow\left[\overrightarrow{AB'};\overrightarrow{BC'}\right]=\left(1;1;1\right)\)
Áp dụng công thức k/c giữa 2 đường thẳng chéo nhau:
\(d\left(AB';BC'\right)=\dfrac{\left|\left[\overrightarrow{AB'};\overrightarrow{BC'}\right].\overrightarrow{AB}\right|}{\left|\left[\overrightarrow{AB'};\overrightarrow{BC'}\right]\right|}=\dfrac{\left|1.1+1.0+1.0\right|}{\sqrt{1^2+1^2+1^2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
Do quy ước mỗi đơn vị độ dài là a nên k/c cần tìm là: \(\dfrac{a\sqrt{3}}{3}\)