
Tổng số học sinh giỏi (kể cả những bạn giỏi cả hai môn): \(25+35=60\left(bạn\right)\)
Số học sinh gồm những bạn giỏi cả Toán và Văn: \(60-45=15\left(bạn\right)\)
Đúng 0
Bình luận (0)
Chọn đúng/sai. giải thích 
a) Đúng \(\)(\(66\) xuất hiện nhiều nhất với 4 lần)
b) Nửa trái gồm \(12\) phần tử: \(59,60,61,63,66,66,66,69,71,72,72,73\)
\(\Rightarrow Q_1=\dfrac{66+66}{2}=66\Rightarrow\) Sai
c) Đúng \(\left(s^2=\dfrac{\sum\left(x_i-\overline{x}\right)^2}{n}=1553\right)\)
d) \(\Delta Q=Q_3-Q_1\)
Nửa trên gồm \(12\) phần tử: \(73,80,81,83,84,85,88,89,93,94,98,265\)
\(\Rightarrow Q_3=\dfrac{85+88}{2}=86,5\)
\(\Rightarrow\Delta Q=86,5-66=20,5\Rightarrow\) Sai
Đúng 0
Bình luận (0)
Giải thích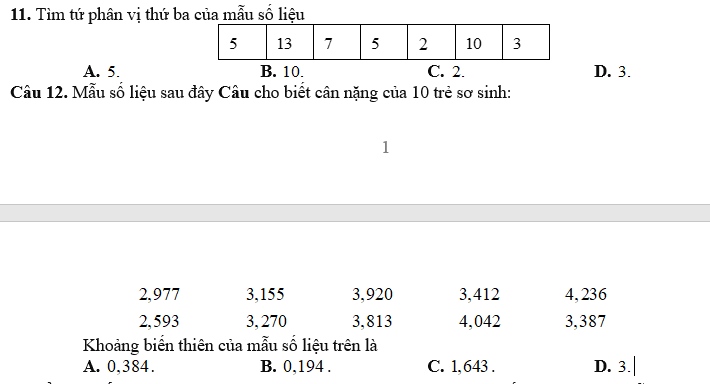
11B \(\left(2;3;5;5;7;10;13\right)\) \(\Rightarrow Q3=10\) \(\left(Q1=3;Q2=5\right)\)
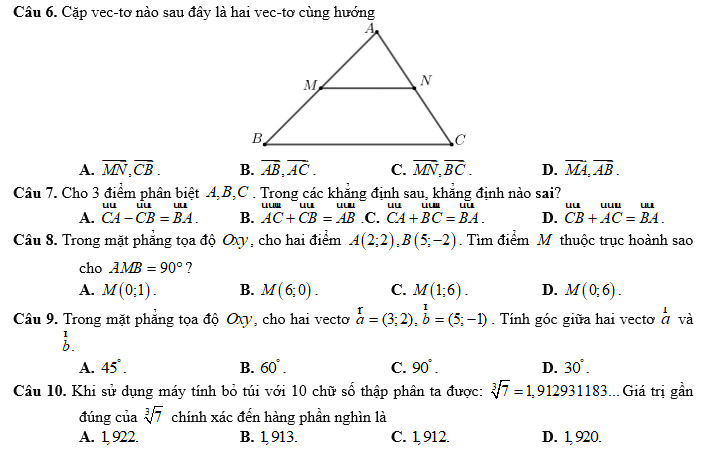
12C \(\left(2,977;3,155;3,920;3,412;4,236;2,593;3,270;3,813;4,042;3,387\right)\)
\(\Rightarrow\) Khoảng biến thiên \(4,236-2,593=1,643\)
Đúng 0
Bình luận (0)
giải thích
giải thích
Giúp e với mn,chi tiết nhé . E sẽ tick sau
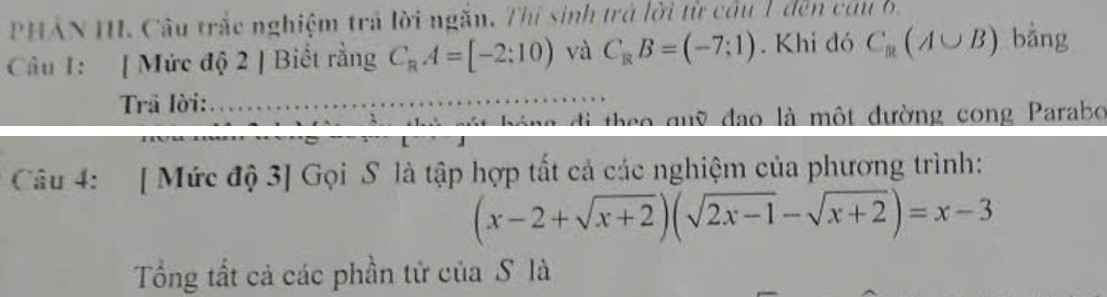
Câu 1:
\(C_RA=[-2;10)\)
=>R\A=[-2;10)
=>A=(-\(\infty\);-2)\(\cup\)[10;+\(\infty\))
\(C_RB=\left(-7;1\right)\)
=>R\B=(-7;1)
=>B=(-\(\infty\);-7]\(\cup\)[1;+\(\infty\))
A\(\cup\)B=(-\(\infty\);-2)\(\cup\)[1;+\(\infty\))
=>\(C_R\left(A\cup B\right)=[-2;1)\)
Đúng 1
Bình luận (0)
help me :<<
Giúp với,được câu nào hay câu đấy
Plz cần gấp!

câu 1: Cho tứ giác ABCD, gọi G là trọng tâm tam giác ABC . Chứng minh:a). vecto AD+vecto CBvecto AB - vecto DCb). vecto AG1/3(vecto AB+vecto AC)câu 2: Một tháp thông tin được xây dựng trên nóc một tòa nhà như hình vẽ. Hỏi tháp cao bao nhiêu mét ?câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có 4(-1;1), B(1;3),C(5,2).a) Tọa độ của vecto AB . Tính chu vi tam giác ABC.b) Tính tích vô hướng vecto AB. vecto BC.c) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Đọc tiếp
câu 1: Cho tứ giác ABCD, gọi G là trọng tâm tam giác ABC . Chứng minh:
a). vecto AD+vecto CB=vecto AB - vecto DC
b). vecto AG=1/3(vecto AB+vecto AC)
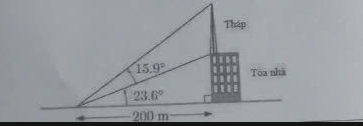
câu 2: Một tháp thông tin được xây dựng trên nóc một tòa nhà như hình vẽ. Hỏi tháp cao bao nhiêu mét ?
câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có 4(-1;1), B(1;3),C(5,2).
a) Tọa độ của vecto AB . Tính chu vi tam giác ABC.
b) Tính tích vô hướng vecto AB. vecto BC.
c) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Câu 1 :
a) \(\overrightarrow{AD}+\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{AD}-\overrightarrow{AB}=-\left(\overrightarrow{DC}+\overrightarrow{CB}\right)\)
\(\Leftrightarrow\overrightarrow{BD}=-\overrightarrow{DB}\left(đúng\right)\)
\(\Rightarrowđpcm\)
b) Ta có \(G\) là trọng tâm \(\Delta ABC\left(gt\right)\)
\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
\(\Leftrightarrow\overrightarrow{0}+\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
\(\Leftrightarrow\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(đpcm\right)\)
Câu 2 :
Chiều cao \(H\) của tháp là :
\(tan\left(23,6^o+15,9^o\right)=\dfrac{H}{200}\)
\(\Leftrightarrow tan39,5^o=\dfrac{H}{200}\)
\(\Leftrightarrow H=200.tan39,5^o\approx165\left(m\right)\)
Đúng 1
Bình luận (1)
Cho tam giác ABC với A (2;4), B(-3;1); C(3;-1)
a) Tính toạ độ điểm D để ABCD là hình bình hành
b) tính toạ độ trọng tâm G của tam giác ABC
c) tính toạ độ trực tâm và tâm đường tròn ngoại tiếp tam giác ABC
a:
A(2;4); B(-3;1); C(3;-1); D(x;y)
\(\overrightarrow{AB}=\left(-3-2;1-4\right)\)
=>\(\overrightarrow{AB}=\left(-5;-3\right)\)
\(\overrightarrow{DC}=\left(3-x;-1-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}3-x=-5\\-1-y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=2\end{matrix}\right.\)
vậy: D(8;2)
b: Tọa độ trọng tâm G của ΔABC là:
\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{2+\left(-3\right)+3}{3}=\dfrac{2}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{4+1+\left(-1\right)}{3}=\dfrac{4}{3}\end{matrix}\right.\)
vậy: \(G\left(\dfrac{2}{3};\dfrac{4}{3}\right)\)
c:
Gọi H(x;y) là tọa độ trực tâm của ΔABC
A(2;4); B(-3;1); C(3;-1); H(x;y)
\(\overrightarrow{AH}=\left(x-2;y-4\right);\overrightarrow{BC}=\left(6;-2\right)\)
\(\overrightarrow{BH}=\left(x+3;y-1\right);\overrightarrow{AC}=\left(1;-5\right)\)
H là trực tâm của ΔABC nên AH\(\perp\)BC; BH\(\perp\)AC
=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6\left(x-2\right)+\left(-2\right)\left(y-4\right)=0\\1\left(x+3\right)+\left(-5\right)\left(y-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x-12-2y+8=0\\x+3-5y+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-2y=12-8=4\\x-5y=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-y=2\\x-5y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{9}{7}\\y=\dfrac{13}{7}\end{matrix}\right.\)
vậy: H(9/7;13/7)
Gọi O(x;y) là tọa độ tâm đường tròn ngoại tiếp ΔABC
O(x;y); A(2;4); B(-3;1); C(3;-1)
\(OA^2=\left(2-x\right)^2+\left(4-y\right)^2=\left(x-2\right)^2+\left(y-4\right)^2\)
\(OB^2=\left(-3-x\right)^2+\left(1-y\right)^2=\left(x+3\right)^2+\left(y-1\right)^2\)
\(OC^2=\left(3-x\right)^2+\left(-1-y\right)^2=\left(x-3\right)^2+\left(y+1\right)^2\)
Vì O là tâm đường tròn ngoại tiếp ΔABC nên OA=OB=OC
=>\(\left\{{}\begin{matrix}\left(x-2\right)^2+\left(y-4\right)^2=\left(x+3\right)^2+\left(y-1\right)^2\\\left(x+3\right)^2+\left(y-1\right)^2=\left(x-3\right)^2+\left(y+1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-4x+4+y^2-8y+16=x^2+6x+9+y^2-2y+1\\x^2+6x+9+y^2-2y+1=x^2-6x+9+y^2+2y+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4x-8y+20=6x-2y+10\\6x-2y+10=-6x+2y+10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-10x+6y=-10\\12x-4y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{4}\\y=-\dfrac{15}{4}\end{matrix}\right.\)
vậy: O(-5/4;-15/4)
Đúng 1
Bình luận (0)









