câu 1: Cho tứ giác ABCD, gọi G là trọng tâm tam giác ABC . Chứng minh:
a). vecto AD+vecto CB=vecto AB - vecto DC
b). vecto AG=1/3(vecto AB+vecto AC)
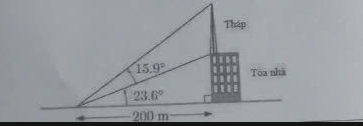
câu 2: Một tháp thông tin được xây dựng trên nóc một tòa nhà như hình vẽ. Hỏi tháp cao bao nhiêu mét ?
câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có 4(-1;1), B(1;3),C(5,2).
a) Tọa độ của vecto AB . Tính chu vi tam giác ABC.
b) Tính tích vô hướng vecto AB. vecto BC.
c) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Câu 1 :
a) \(\overrightarrow{AD}+\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{AD}-\overrightarrow{AB}=-\left(\overrightarrow{DC}+\overrightarrow{CB}\right)\)
\(\Leftrightarrow\overrightarrow{BD}=-\overrightarrow{DB}\left(đúng\right)\)
\(\Rightarrowđpcm\)
b) Ta có \(G\) là trọng tâm \(\Delta ABC\left(gt\right)\)
\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
\(\Leftrightarrow\overrightarrow{0}+\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
\(\Leftrightarrow\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(đpcm\right)\)
Câu 2 :
Chiều cao \(H\) của tháp là :
\(tan\left(23,6^o+15,9^o\right)=\dfrac{H}{200}\)
\(\Leftrightarrow tan39,5^o=\dfrac{H}{200}\)
\(\Leftrightarrow H=200.tan39,5^o\approx165\left(m\right)\)














