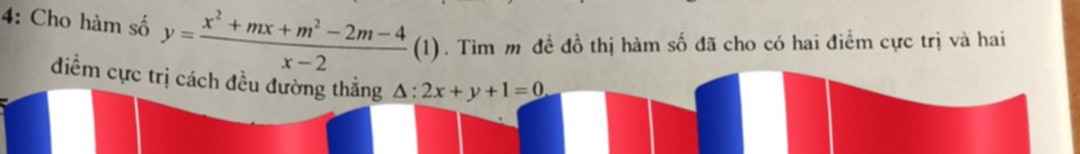
\(y'=\dfrac{x^2-4x-2m+2m+4}{\left(x-2\right)^2}=\dfrac{x^2-4x+4}{\left(x-2\right)^2}=1>0,\forall x\ne2\)

\(\Rightarrow\left(1\right)\) đồng biến trên \(D=R|\left\{2\right\}\)

\(\Rightarrow\) Hàm số cho không có 2 điểm cực trị

Vậy không tồn tại bất kì giá trị \(m\) nào thỏa mãn đề bài

\(y'=h'\left(x\right)=3x^2-12x\)

\(h'\left(x\right)=0\Leftrightarrow3x^2-12x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Lập BBT ta thấy hàm số \(h\left(x\right)\) đạt cực đại tại \(x=0\) và đạt cực tiểu tại \(x=4\)

\(h\left(x\right)_{max}=h\left(0\right)=0^3=6.0^2+100=100\left(km\right)\)

\(h\left(x\right)_{min}=h\left(4\right)=4^3=6.4^2+100=68\left(km\right)\)

Khoảng cách từ đỉnh núi \(\left(0;100\right)\) đến thung lũng sâu nhất \(\left(4;68\right)\) là:

\(d=\sqrt{\left(4-0\right)^2+\left(68-100\right)^2}\approx32,25\left(km\right)\)

Không có hình vẽ

Theo đề bài ta có tọa độ :

\(O\left(0;0;0\right)\)

\(A=\left(2;0;0\right)\)

\(B\left(0;3;0\right)\)

\(OO'=4\) và \(\left(\widehat{OO';\left(OAB\right)}\right)=30^o\)

Chiếu \(\overrightarrow{OO'}\) lên mặt phẳng đáy trục \(xy:\) \(\left|OO'_{xy}\right|=OO'.cos30^o=4.\dfrac{\sqrt{3}}{2}=2\sqrt{3}\)

Chiếu \(\overrightarrow{OO'}\) lên trục \(Oz:\left|OO'_{Oz}\right|=OO'.sin30^o=4.\dfrac{1}{2}=2\)

\(\Rightarrow O'\left(0;0;2\right)\)

Điểm \(B'\left(a;b;c\right)\) là ảnh của điểm \(B\left(0;3;0\right)\) theo phép tịnh tiến \(\overrightarrow{OO'}\)

\(\Rightarrow\left\{{}\begin{matrix}a=0+0=0\\b=3+0=3\\c=0+2=2\end{matrix}\right.\) 

\(\Rightarrow B'\left(0;3;2\right)\)

\(\Rightarrow S=b+c=3+2=5\)

\(f\left(x\right)=\left|2x-3\right|=\left[{}\begin{matrix}2x-3\left(x\ge\dfrac{3}{2}\right)\\-2x+3\left(x< \dfrac{3}{2}\right)\end{matrix}\right.\)

\(\Rightarrow F\left(x\right)=\left[{}\begin{matrix}\int\left(2x-3\right)dx=x^2-3x+C_1\left(x\ge\dfrac{3}{2}\right)\\\int\left(-2x+3\right)dx=-x^2+3x+C_2\left(x< \dfrac{3}{2}\right)\end{matrix}\right.\)

\(F\left(2\right)=4\Leftrightarrow2^2-3.2+C_1=4\Leftrightarrow C_1=6\)

\(\Rightarrow F\left(x\right)=x^2-3x+6\left(x\ge\dfrac{3}{2}\right)\)

\(\Rightarrow F\left(4\right)=4^2-3.4+6=10\)

Để Hs \(F\left(x\right)\) liên tục tại \(x=\dfrac{3}{2}\) khi và chỉ khi

\(\Leftrightarrow\lim\limits_{x\rightarrow\dfrac{3}{2}^+}F\left(x\right)=\lim\limits_{x\rightarrow\dfrac{3}{2}^-}F\left(x\right)\)

\(\Leftrightarrow\left(\dfrac{3}{2}\right)^2-3.\dfrac{3}{2}+6=-\left(\dfrac{3}{2}\right)^2+3.\dfrac{3}{2}+C_2\)

\(\Leftrightarrow C_2=6\)

\(\Rightarrow F\left(x\right)=-x^2+3x+6\left(x< \dfrac{3}{2}\right)\)

\(\Rightarrow F\left(-1\right)=-\left(-1\right)^2+3.\left(-1\right)+6=2\)

Vậy \(2F\left(-1\right)+F\left(4\right)=2.2+10=14\)

Chiều cao ra đa trên đỉnh tháp là \(90\left(m\right)=0,09\left(km\right)\)

\(\Rightarrow\) tọa độ của radar là \(O'\left(0;0;0,09\right)\)

Tọa độ của máy bay \(A\) là \(A\left(-350;-250;15\right)\)

Khoảng cách từ máy bay \(A\) đến radar là 

\(O'A=\sqrt{\left(-350-0\right)^2+\left(-250-0\right)^2+\left(15-0,09\right)^2}=430,5\approx431\left(km\right)\)

Ta có :

\(\overrightarrow{AC'}=\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{AA'}\) ( Quy tắc hình hộp chữ nhật)

\(\Rightarrow\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\)

\(\Rightarrow F^2=F_1^2+F_2^2+F_3^2\left(\overrightarrow{F_1}\perp\overrightarrow{F_2}\perp\overrightarrow{F_3}\right)\)

\(\Rightarrow F^2=4^2+6^2+8^2=116\)

\(\Rightarrow F\approx10,8\approx11\left(N\right)\)

Ta có hệ cân bằng khi và chỉ khi

\(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\overrightarrow{P}=\overrightarrow{0}\)

Chiếu lên phương đứng ta được :

\(F_1.cos45^o+F_2.cos45^o+F_3.cos45^o-P=0\)

\(\Leftrightarrow P=3F_1cos45^o=3.10.\dfrac{\sqrt{2}}{2}=15\sqrt{2}\approx21,2\left(N\right)\)