Mất gốc toán mà sắp thi rồi ai chỉ mẹo với
Cho hình chóp S.ABC là tam giác đều. Gọi M,N,Q lần lượt là trung điểm của BC, AB, AC : Chứng minh
a) BC ⊥ SM
b) CN ⊥SB
c) BQ ⊥ SC
Half time show của Super Bowl 2023 thuộc về ngôi sao nhạc pop Rihanna. Màn trình diễn của cô gây ấn tượng mạnh mẽ trên 77 nền sân khấu lơ lửng ở độ cao từ 4,5m4,5m đến 18m18m. Mỗi nền sân khấu được gắn đèn LED nhấp nháy giống như Rihanna đang biểu diễn trên những đám mây. Để có thể tạo được sân khấu có hiệu ứng tốt mà vẫn đảm bảo an toàn, sân khấu sẽ được kết nối bởi 4 sợi dây cáp có ròng rọc lên một khung sắt chắc chắn sao cho hình chiếu của ròng rọc luôn nằm ở trung điểm các viền của sân khấu...
Đọc tiếp
Half time show của Super Bowl 2023 thuộc về ngôi sao nhạc pop Rihanna. Màn trình diễn của cô gây ấn tượng mạnh mẽ trên nền sân khấu lơ lửng ở độ cao từ đến . Mỗi nền sân khấu được gắn đèn LED nhấp nháy giống như Rihanna đang biểu diễn trên những đám mây. Để có thể tạo được sân khấu có hiệu ứng tốt mà vẫn đảm bảo an toàn, sân khấu sẽ được kết nối bởi 4 sợi dây cáp có ròng rọc lên một khung sắt chắc chắn sao cho hình chiếu của ròng rọc luôn nằm ở trung điểm các viền của sân khấu ( minh họa như hình vẽ ). Khi sân khấu chạm mặt đất, độ cao từ khung sắt đến sân khấu là , độ dài dây cáp lúc này được điều chỉnh thành . Khí đó góc tạo bởi dây cáp và sân khấu sẽ có giá trị là ?

Cho hình chóp SABCD có đáy ABCD là hình vuông tâm O cạnh bên SA vuông góc với ABCD tìm góc giữa SAC và SAD
Gọi cạnh hình vuông \(ABCD\) là \(a;SA=h\)
Chọn hệ trục tọa độ \(Oxyz:A\left(0;0;0\right);B\left(a;0;0\right);C\left(a;a;0\right);D\left(0;a;0\right);S\left(0;0;h\right)\)
\(\overrightarrow{SA}=\left(0;0;-h\right);\overrightarrow{SC}=\left(a;a;-h\right);\overrightarrow{SD}=\left(0;a;-h\right)\)
\(\Rightarrow\overrightarrow{n\left(SAC\right)}=\overrightarrow{n_1}=\left[\overrightarrow{SA}.\overrightarrow{SC}\right]=\left(0;-ah;ah\right)=\left(0;-1;1\right)\)
\(\overrightarrow{n\left(SAD\right)}=\overrightarrow{n_2}=\left[\overrightarrow{SA}.\overrightarrow{SD}\right]=\left(0;0;ah\right)=\left(0;0;1\right)\)
\(cos\left(\widehat{\left(SAC\right);\left(SAD\right)}\right)=\dfrac{\overrightarrow{n_1}.\overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\dfrac{0.0+\left(-1\right).0+1.1}{\sqrt{0^2+\left(-1\right)^2+1^2}.\sqrt{0^2+0^2+1^2}}=\dfrac{\sqrt[]{2}}{2}\)
\(\Rightarrow\left(\widehat{\left(SAC\right);\left(SAD\right)}\right)=45^o\)
Đúng 0
Bình luận (1)
Cho tứ diện OABC có OA OB OC , , đôi một vuông góc với nhau và OA OB OC 1.a) Tính góc giữa hai đường thẳng AB và AC.b) Gọi M là trung điểm của cạnh BC. Hãy tính góc giữa hai đường thẳng AB và OM.
Đọc tiếp
Cho tứ diện OABC có OA OB OC , , đôi một vuông góc với nhau và OA =OB =OC =1.
a) Tính góc giữa hai đường thẳng AB và AC.
b) Gọi M là trung điểm của cạnh BC. Hãy tính góc giữa hai đường thẳng AB và OM.
a) Ta chọn hệ tọa độ \(Oxyz:O\left(0;0;0\right);A\left(1;0;0\right);B\left(0;1;0\right);C\left(0;0;1\right)\)
\(\overrightarrow{AB}=\left(-1;1;0\right)\)
\(\overrightarrow{AC}=\left(-1;0;1\right)\)
\(cos\left(\widehat{\overrightarrow{AB};\overrightarrow{AC}}\right)=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=\dfrac{\left(-1\right).\left(-1\right)+1.0+0.1}{\sqrt{\left(-1\right)^2+1^2+0^2}.\sqrt{\left(-1\right)^2+0^2+1^2}}=\dfrac{1}{2}\)
\(\Rightarrow\left(\widehat{\overrightarrow{AB};\overrightarrow{AC}}\right)=60^o\)
b) \(M\) là trung điểm \(BC\Rightarrow M\left(\dfrac{0+0}{2};\dfrac{1+0}{2};\dfrac{0+1}{2}\right)=\left(0;\dfrac{1}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{OM}=\left(0;\dfrac{1}{2};\dfrac{1}{2}\right)\)
\(cos\left(\widehat{\overrightarrow{AB};\overrightarrow{OM}}\right)=\dfrac{\overrightarrow{AB}.\overrightarrow{OM}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{OM}\right|}=\dfrac{\left(-1\right).0+1.\dfrac{1}{2}+0.\dfrac{1}{2}}{\sqrt{\left(-1\right)^2+1^2+0^2}.\sqrt{0^2+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^2}}=\dfrac{1}{2}\)
\(\Rightarrow\left(\widehat{\overrightarrow{AB};\overrightarrow{OM}}\right)=60^o\)
Đúng 1
Bình luận (0)
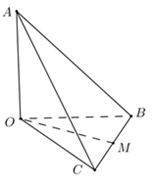
a) Do OA=OB=OC
⇒AB=AC=BC ⇒ΔABC đều
=> (AB,AC) = BAC = 60o
b) Gọi N là trung điểm của AC ⇒MN//AB
Ta có
![]()
Vậy ∆OMN là tam giác đều => OMN=60o
Đúng 1
Bình luận (0)
Giải giúp vs mn
Bài 2. Cho tứ diện \(ABCD\) có \(AB = CD = 2a\), \(M\) là trung điểm của \(BC\), \(AD\) tính góc giữa \(AD, CD\). Gọi \(MN\) giao tuyến của...
Bổ sung độ dài \(MN\)
Gọi \(P\) là trung điểm \(BD\)
Ta có \(MP//CD;NP//AB\) (đường trung bình)
\(\Rightarrow\left(\widehat{AB;CD}\right)=\left(\widehat{MP;NP}\right)\)
mà \(MP=NP=a\) (đường trung bình)
\(cos\widehat{MPN}=\dfrac{MP^2+NP^2-MN^2}{2.MP.NP}=...\)
\(\Rightarrow\widehat{MPN}=...\)
\(\Rightarrow\left(\widehat{AB;CD}\right)=\left(\widehat{MP;NP}\right)=180^o-\widehat{MPN}=...\) (Nếu \(\widehat{MPN>90^o}\))
Đúng 1
Bình luận (3)
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy là hình thang vuông tại A, có đáy lớn AB, AB = 2a, AD = DC = a. Vẽ AH ⊥ SC, H ∈ SC và M là trung điểm AB. Biết [S, DC, B] = 60°. Gọi Sx là giao tuyến của (SAD) và (SMC). Tính [A, Sx, M]
giúp em với đi ạ!!!!!!!!!!!!!!!!
Chọn hệ trục tọa độ :
\(A(0;0;0);B(2𝑎;0;0);D(0;𝑎;0);C(2𝑎;𝑎;0)\)
\(S\left(0;0;h\right)\) với \(SA\perp\left(ABCD\right)\)
\(M\left(a;0;0\right)\) (\(M\) là trung điểm \(AB\))
Ta có \(\left[S;DC;B\right]=60^o\Rightarrow cos60^o=\dfrac{\left|\overrightarrow{SD}.\overrightarrow{n}\right|}{SD.n}\)
\(\overrightarrow{DC}=\left(2a;0;0\right);\overrightarrow{DB}=\left(2a;-a;0\right)\)
\(\overrightarrow{n}=\overrightarrow{DC}.\overrightarrow{DB}=\left(0;0;-2a^2\right)\)
\(\Rightarrow\overrightarrow{SD}=\left(0;a;h\right)\Rightarrow SD=\sqrt{a^2+h^2};n=2a^2\)
\(\Rightarrow\overrightarrow{SD}.\overrightarrow{n}=\left(0;a;h\right).\left(0;0;-2a^2\right)=-2a^2h\)
\(\Rightarrow cos60^o=\dfrac{h}{\sqrt{a^2+h^2}}\Rightarrow h=\dfrac{a}{\sqrt{3}}\)
Xét \(\left(SAD\right):S\left(0;0;h\right);A\left(0;0;0\right);D\left(0;a;0\right)\)
\(x=0\Rightarrow\left(SAD\right):x=0\)
Xét \(\left(SMC\right):S\left(0;0;h\right);M\left(a;0;0\right);C\left(2a;a;0\right)\)
\(\overrightarrow{SM}=\left(a;0;-h\right);\overrightarrow{SC}=\left(2a;a;-h\right)\)
\(\Rightarrow\overrightarrow{n_{PT}}=\left(ah;ah;a^2\right)\)
\(\Rightarrow\left(SMC\right):hx+hy+az=ah\)
Giao tuyến của \(x=0\) và \(\left(SMC\right)\) là : \(hy+az=ah\)
\(\Rightarrow\left(Sx\right):\left\{{}\begin{matrix}y=t\\z=\dfrac{ah-ht}{a}\end{matrix}\right.\)
\(d\left(A;Sx\right)=\dfrac{h^2}{a\sqrt{1+\dfrac{h^2}{a^2}}}\)
Với \(h^2=\dfrac{1}{3}a^2\Rightarrow d\left(A;Sx\right)=\dfrac{\dfrac{a^2}{3}}{a\sqrt{\dfrac{4}{3}}}=\dfrac{a\sqrt{3}}{6}\)
Đúng 1
Bình luận (0)
Cho hình chóp OABC có OA,OB, OC đôi một vuông góc và OA = OB = OC = a. Gọi M là điểm nằm trên cạnh BC sao cho BM = 2 MC, alpha là góc giữa hai đường thẳng AB và OM. Tính cos alpha?
Cho hình chóp S.ABCD, đáy là hình vuông cạnh a, SA = SB = SC = 3a, điểm M thuộc cạnh BC thỏa mãn BM = 2 MC. Góc alpha là góc tạo bởi SB và DM. Tính alpha đó.
Cho hình hóp S.ABCD, có đáy ABCD là hình thang vuông tại A và D. Gọi E là trung điểm của AB. Biết AB 2a, AD DC a, đồng thời SA vuông góc AB, SA vuông góc AD và SA dfrac{2asqrt{3}}{3}. Khi đóCác mệnh đề sau đúng hay sai?a) (SB, DC ) widehat{SBA}b) tanwidehat{SBA}dfrac{sqrt{3}}{2}c) DE song song BCd) (SD,BC) xấp xỉ 52,42^o
Đọc tiếp
Cho hình hóp S.ABCD, có đáy ABCD là hình thang vuông tại A và D. Gọi E là trung điểm của AB. Biết AB = 2a, AD = DC = a, đồng thời SA vuông góc AB, SA vuông góc AD và SA = \(\dfrac{2a\sqrt{3}}{3}\). Khi đó
Các mệnh đề sau đúng hay sai?
a) (SB, DC ) = \(\widehat{SBA}\)
b) \(tan\widehat{SBA}=\dfrac{\sqrt{3}}{2}\)
c) DE song song BC
d) (SD,BC) xấp xỉ \(52,42^o\)
a, Đ
Vì DC // AB (do ABCD là hình thang), góc giữa SB và DC bằng góc giữa SB và AB, tức là \(\widehat{SBA}\)
b, S
\(\Delta\)SAB \(\perp\) A, ta có
\(tan\widehat{SBA}\) = \(\dfrac{SA}{AB}\) = \(\dfrac{\text{2a√3}}{\dfrac{3}{2a}}\) =\(\dfrac{\text{ √3}}{3}\)
c, S
Gọi F là TĐ của AB. Khi đó, \(AF = FB = a\).
Xét hình thang ABCD, ta có:
\(AD = DC = a, AB = 2a.\)
Suy ra, \(\text{AF = AD = DC = a.}\)
Tứ giác AFCD là hình vuông.
Ta có: \(AE = EB = a, AF = AD = a.\)
Xét \(\Delta\) ADE và \(\Delta\) CBF, ta thấy chúng không đồng dạng, do đó DE không // BC.
d, S
≈ 74,99°
Đúng 1
Bình luận (0)











