Cho cota=-2.tìm các giá trị lượng giác
Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
Hỏi đáp
cos 0 + cos 20 + cos 40 +...+ cos 160 + cos 180
=cos0+cos180+cos20+cos160+cos40+cos140+cos60+cos120+cos80+cos100
=0+0+...+0
=0
Đúng 0
Bình luận (0)
`cos 0^o +cos 20^o +cos 40^o +...+cos 160^o +cos 180^o`
`=(cos 0^o +cos 180^o)+(cos 20^o +cos 160^o)+....+(cos 80^o +cos 100^o)`
`=(cos 0^o -cos 0^o)+(cos 20^o -cos 20^o)+....+(cos 80^o -cos 80^o)`
`=0`
Áp dụng: `cos \alpha = -cos(180^o -\alpha)=-cos(\pi - \alpha)`.
Đúng 0
Bình luận (0)
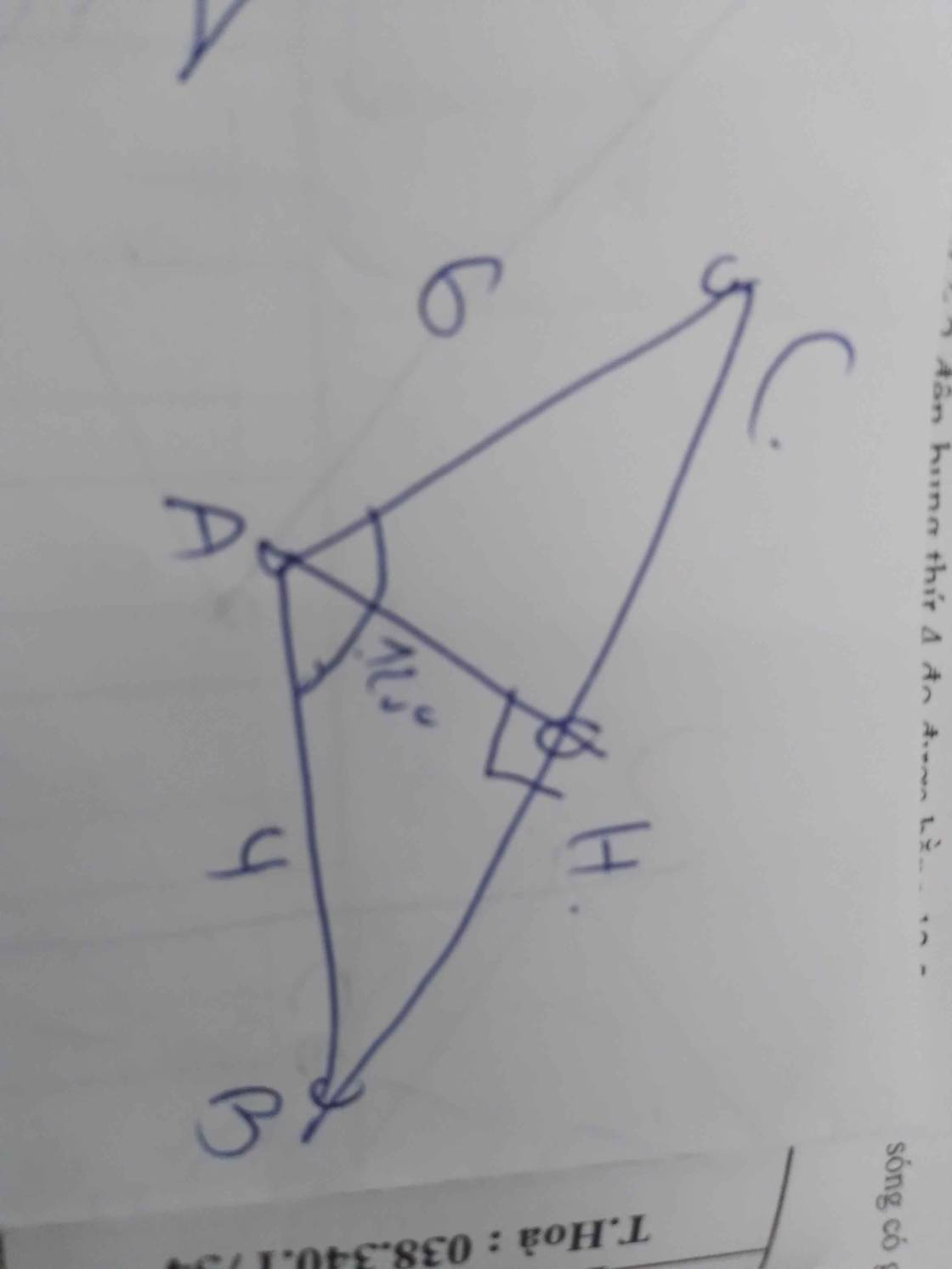
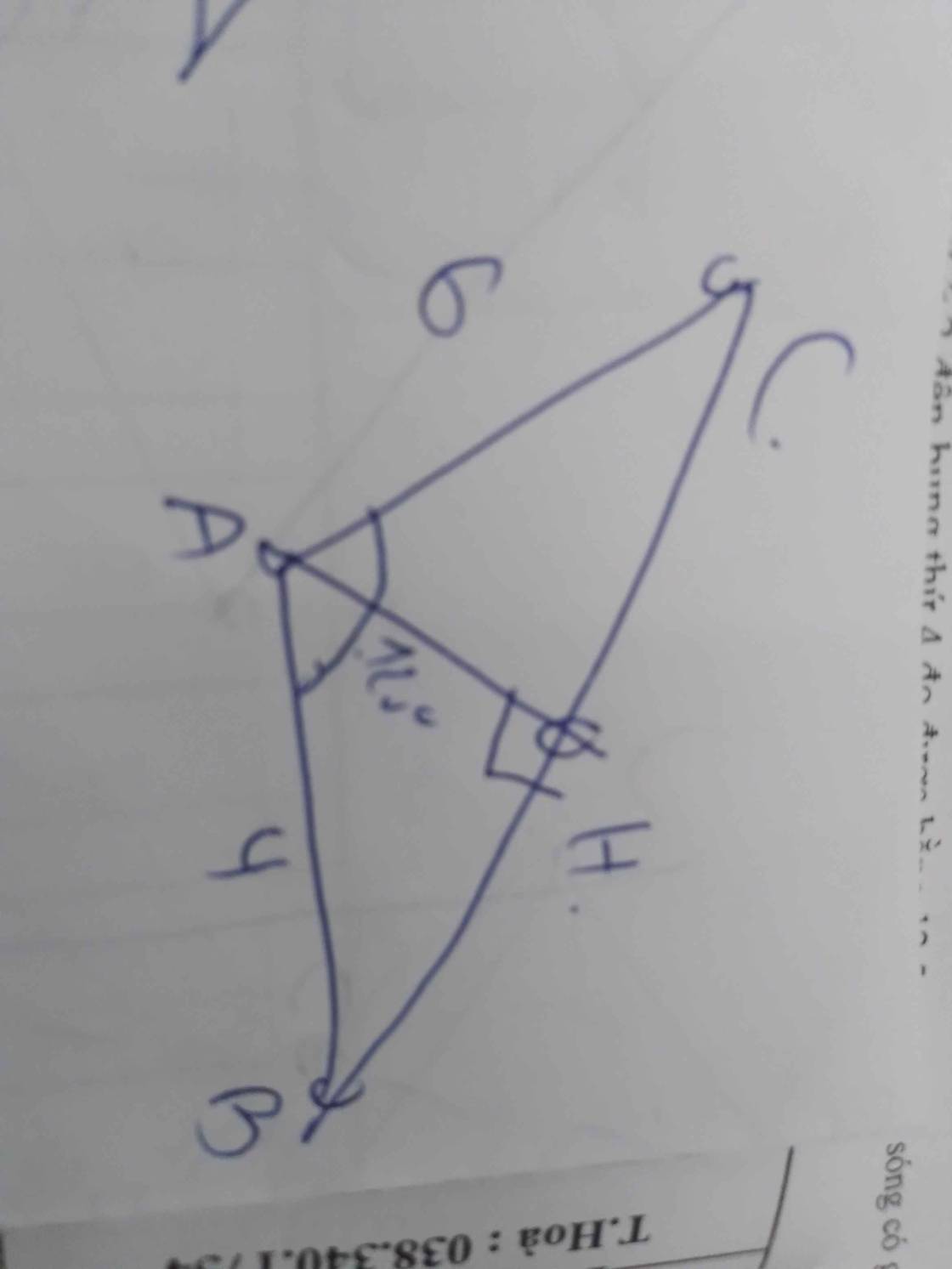
Cho ∆ABC có a=2√3cm, c=2cm, góc B=30° a) giải ∆ABC b) Tính S, hc, mb
a: Xét ΔABC có
\(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{4+12-AC^2}{2\cdot2\cdot2\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(16-AC^2=4\cdot2\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=12\)
\(\Leftrightarrow AC^2=4\)
=>AC=2
Xét ΔABC có AB=AC
nên ΔABC cân tại A
=>\(\widehat{BAC}=\dfrac{180^0-\widehat{B}}{2}=120^0\)
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=30^0\)
b: Kẻ CH vuông góc AB
=>CH=hC
\(\widehat{CAH}+\widehat{CAB}=180^0\)(hai góc kề bù)
=>\(\widehat{CAH}+120^0=180^0\)
=>\(\widehat{CAH}=60^0\)
Xét ΔCAH vuông tại H có \(sinCAH=\dfrac{CH}{CA}\)
=>\(\dfrac{CH}{1}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(CH=\dfrac{\sqrt{3}}{2}\)
Gọi M là trung điểm của AC
=>BM=mb
M là trung điểm của AC
=>AM=AC/2=1
Xét ΔAMB có \(cosMAB=\dfrac{AM^2+AB^2-MB^2}{2\cdot MA\cdot AB}\)
=>\(\dfrac{1^2+2^2-MB^2}{2\cdot1\cdot2}=cos120=\dfrac{-1}{2}\)
=>\(5-MB^2=-2\)
=>\(MB^2=7\)
=>\(MB=\sqrt{7}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 4 AC = 6 A = 120 độ Tính BC,S,ha,R.
x34π3�10�7 b)y19900
Đọc tiếp
b)
Đề chỉ ghi mỗi như thế này thôi, bạn muốn làm gì với những dữ kiện này nhỉ?
Đúng 0
Bình luận (0)
GÓC HÌNH HỌC CÓ SỐ ĐO TỪ 0 ĐÔ ĐẾN 180 ĐỘ HAY TỪ 0 ĐỘ ĐẾN 360 ĐỘ?
rút gọn biểu thức \(S=sin\left(x+2017\pi\dfrac{ }{ }2\right)+2sin^2\left(x-\pi\right)+cos\left(x+2019\pi\right)+cos2x\)
trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng Δ :\(x-2y-5=0\) và các điểm A(1;2) , B(-2;3) , C(-2;1) . Viết phương trình đường thẳng \(d\), biết đường thẳng \(d\) đi qua gốc tọa độ và cắt đường thẳng Δ tại điểm M sao cho : \(\left|\overline{MA}+\overline{MB}+\overline{MC}\right|\)nhỏ nhất
Rút gọn biểu thức
\(1-\dfrac{sin^2x}{1+cotx}-\dfrac{cos^2x}{1+tanx}\)
bạn chỉ cần nhớ rằng: sin2x+ cos2x= 1 và cotx*tanx= 1 rồi quy đồng lên và làm bình thường
Đúng 0
Bình luận (0)
\(=\dfrac{1+cotx-sin^2x}{1+\dfrac{cosx}{sinx}}-\dfrac{cos^2x}{1+\dfrac{sinx}{cosx}}\)
\(=\left(1+\dfrac{cosx}{sinx}-sin^2x\right):\dfrac{sinx+cosx}{sinx}-cos^2x:\dfrac{cosx+sinx}{cosx}\)
\(=\dfrac{sinx+cosx-sin^3x}{sinx}\cdot\dfrac{sinx}{sinx+cosx}-\dfrac{cos^3x}{cosx+sinx}\)
\(=\dfrac{sinx+cosx-sin^3x-cos^3x}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)-\left(sinx+cosx\right)\left(sin^2+cos^2x-sinx\cdot cosx\right)}{sinx+cosx}\)
\(=1-1+sinx\cdot cosx=\dfrac{1}{2}sin2x\)
Đúng 0
Bình luận (0)