Bài 8: Vị trí tương đối của hai đường tròn (Tiếp)

a: Xét (O) có

MC,MA là tiếp tuyến

=>MC=MA

=>OM là trung trực của AC và OM là phân giác của góc COA(1)

Xét (O') có

MA,MD là tiếp tuyến

=>MA=MD và O'M là phân giác của góc AO'D(2)

góc MOO'+góc MO'O

=1/2(góc COO'+góc DO'O)

=1/2*180=90 độ

=>ΔOMO' vuông tại M

Xét ΔOMO' vuông tại M và ΔCAD vuông tại A có

góc MOO'=góc ACD

=>ΔOMO' đồng dạng với ΔCAD

b: MA=căn R*R'

=>CD=2*căn R*R'

c) sin 15⁰ + sin 75⁰ - cos 15⁰ - cos 75⁰ + sin 30⁰

= sin 15⁰ + sin 75⁰ - sin 75⁰ - sin 15⁰ + sin 30⁰

= (sin 15⁰ - sin 15⁰) + (sin 75⁰ - sin 75⁰) + sin 30⁰

= 0 + 0 + 1/2

= 1/2

a: Xét tứ giác ODKA co

góc KAO+góc KDO=180 độ

=>ODKA là tứ giác nội tiếp

b: Xét (O) có

KD,KA là tiếp tuyến

=>KD=KA và KO là phân giác của góc DKA(1) và OK là phân giác của góc DOA(3)

Xét (O') có

KA,KE là tiếp tuyến

nên KA=KE và KO' là phân giác của góc AKE(2) và O'K là phân giác của góc AO'E(4)

KA=KE

KD=KA
=>KE=KD

=>K là trung điểm của ED

Từ (1), (2) suy ra góc OKO'=1/2*180=90 độ

c: Từ (3), (4) suy ra góc KOO'+góc KO'O=1/2*180=90 độ

=>góc OKO'=90 độ

=>\(KA=\sqrt{3\cdot9}=3\sqrt{3}\left(cm\right)\)

=>\(DE=6\sqrt{3}\left(cm\right)\)

d: Xét ΔADE có

AK là trung tuyến

AK=DE/2

=>ΔADE vuông tại A

e: KD=KA

OA=OD

=>KO là trung trực của AD

=>KO vuông góc AD

KA=KE

O'A=O'E

=>KO' là trung trực của AE

=>KO' vuông góc AE

Xét tứ giác AIKJ có

góc AIK=góc AJK=góc IKJ=90 độ

=>AIKJ là hình chữ nhật

lên cả bàn gv chụp lại ngầu đét 

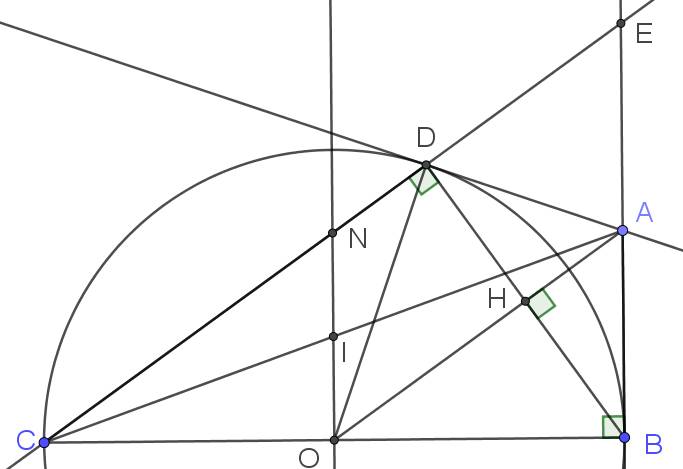
a) Trong tam giác $BCD$ có $OC=OB=OD (=R)$, do đó tam giác BCD vuông tại D.

b) Áp dụng tính chất hai tiếp tuyến $AD$ và $AB$ cắt nhau tại $A$, ta có $AB=AD$. 

Mặt khác $OB=OD$, do đó $OA$ là đường trung trực của $BD$, từ đây suy ra $OA$ vuông góc với $BD$.

Áp dụng hệ thức lượng trong tam giác vuông $ODA $ vuông tại $D$:

$R^2 = OD^2 = OH . OA$

c) $CD$ cắt $AB$ tại $E$.

Tam giác $ABD$ cân tại $A$(chứng minh trên), suy ra $\widehat{ADB}$ $=$ $\widehat{ABD}$.

Mặt khác, ta có

$\widehat{DEA} + \widehat{DBA}=90^{o}$, do đó $\widehat{DEA} + \widehat{ADB}=90^{o}$.

mà $\widehat{EDA} + \widehat{ADB}=90^{o}$.

Suy ra $\widehat{DEA}=\widehat{EDA}$, suy ra tam giác DEA cân tại A, suy ta $AD=AE=AB$. (*)

Áp dụng định lí Ta-let cho tam giác $CAE$ và tam giác $CBA$.

\(\dfrac{OI}{AB}=\dfrac{IN}{EA}\left(=\dfrac{CI}{CA}\right)\)

Từ đây, do (*), nên ta có $OI=IN$, ta suy ra điều cần chứng minh.

a: Xét tứ giác OAKD có

góc OAK+góc ODK=180 độ

=>OAKD là tứ giác nội tiếp

b: Xét (O) có

KD,KA là tiếp tuyến

nên KD=KA và KO là phân giác của góc DKA(1)

Xét (O) có

KA,KE là tiếp tuyến

nên KA=KE và KO' là phân giác của góc AKE(2)

KD=KA

KE=KA
=>KE=KD

=>K là trug điểm của DE

Từ (1), (2) suy ra góc OKO'=1/2*180=90 độ

d: Xet ΔDAE có

AK là trung tuyến

AK=DE/2

=>ΔDAE vuông tại A