Cho 2 đường tròn (O;6 cm) và (O'4 cm) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B ∈ (O), C ∈ (O'). Tiếp tuyến chung trong A cắt tiếp tuyến chung ngoại BC tại I
a) Chứng minh ΔOIO' là Δ vuông
b) Chứng minh OO' là tiếp tuyến của đường tròn ngoại tiếp ΔABC
Bài 8: Vị trí tương đối của hai đường tròn (Tiếp)
a: Xét (O) có
IB,IA là tiếp tuyến
nên IB=IA và IO là phân giác của góc BIA(1)
Xét (O') có
IA,IC là tiếp tuyến
nên IA=IC và IO' là phân giác của gócc AIC(2)
Từ (1), (2) suy ra góc OIO'=1/2*180=90 độ
b: Xét ΔABC có
AI là trung tuyến
AI=BC/2
=>ΔABC vuông tại A
=>I là tâm đường tròn ngoại tiếp ΔABC
Gọi H là trung điểm của OO'
Xét hình thang OBCO' có
I,H lần lượt là trung điểm của BC,OO'
nên IH là đường trung bình
=>IH//OB//O'C
=>IH vuông góc BC
=>OO' là tiếp tuyến của (I)
Đúng 0
Bình luận (0)
Hai (O) và (O') cắt nhau ở A và B (O và O' thuộc 2 nửa mp bờ AB). Kẻ các đường kính BOC và BO'D
a, C/m: 3 điểm C,A,D thẳng hàng
b, Biết OO'= 5cm, OB= 4cm, O'B= 3cm. Tính diện tích tam giác ABC
Em cần gấpp lắm huhu
a: góc CAB=1/2*sđ cung CB=90 độ
góc BAD=1/2*sđ cung BD=90 độ
góc CAD=góc CAB+góc BAD
=90 độ+90 độ=180 độ
=>C,A,D thẳng hàng
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, vẽ tia Ox cố định và lấy A di chuyển trên tia đó.Dựng BC là tiếp tuyến chung ngoài của(O) và (A,AO) với B, C là các tiếp điểm (B∈(O), C∈(A)).Chứng minh rằng C nằm trên đường thẳng cố định khi A di chuyển.
Em cảm ơn!
Để chứng minh rằng C nằm trên đường thẳng cố định khi A di chuyển, ta sẽ sử dụng tính chất của tiếp tuyến và đường tròn. Gọi M là giao điểm của đường thẳng BC và đường tròn (O). Ta cần chứng minh rằng M nằm trên đường thẳng cố định khi A di chuyển. Vì BC là tiếp tuyến chung ngoài của (O) và (A, AO), nên ta có: ∠CMB = ∠CAB (cùng nằm ở cùng một cung CM trên đường tròn (O)) ∠CMB = ∠BAC (do BC là tiếp tuyến chung ngoài của (O) và (A, AO)) Từ hai phương trình trên, ta có: ∠CAB = ∠BAC Điều này cho thấy ∠CAB và ∠BAC là hai góc bằng nhau, nên ta có thể kết luận rằng M nằm trên đường thẳng cố định khi A di chuyển. Vậy, chúng ta đã chứng minh được rằng C nằm trên đường thẳng cố định khi A di chuyển.
Đúng 1
Bình luận (1)
1) Cho (I;2cm) (O) đường kính 8cm tiếp xúp tại C, AB là tiếp tuyến của hai đường tròn. Tính tứ giác ABOI
2) Cho (O;3cm)(I;1cm) tiếp xúp tại C tiếp tuyến chung AB của hai đường tròn cắt OI tại M. Tính MC
3) Cho (O;12cm)(O'16cm) chát nhau tại A và B sao cho OA là tiếp tuyến của đường tròn (O'). Tính dây AB
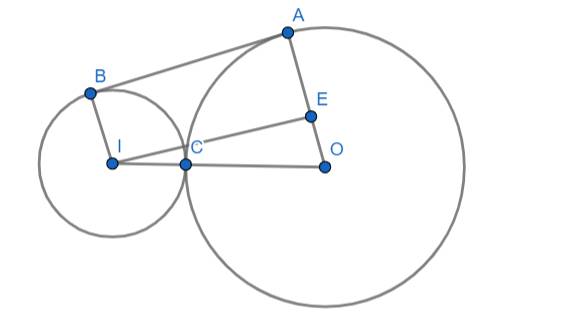
Do AB là tiếp tuyến chung của (O) và (I) nên:
\(\left\{{}\begin{matrix}\widehat{IBA}=90^o\\\widehat{OAB}=90^o\end{matrix}\right.\) (tiếp tuyến vuông góc với bán kính)
\(\Rightarrow\left\{{}\begin{matrix}IB\perp AB\\OA\perp AB\end{matrix}\right.\)
\(\Rightarrow IB//OA\) (cùng vuông góc với AB)
\(\Rightarrow ABOI\) là hình thang
Ta kẻ IE vuông góc với OA tại E
⇒ IEAB là hình chữ nhật
⇒ \(IB=AE=2\left(cm\right)\) (cặp cạnh đối của hình chữ nhật)
\(\Rightarrow OE=OA-AE=8-2=6\left(cm\right)\)
Mà: \(OI=OC+IC=2+8=10\left(cm\right)\)
Xét ΔIEO vuông tại E áp dụng định lý Py-ta-go ta có:
\(IO^2=OE^2+IE^2\)
\(\Leftrightarrow10^2=6^2+IE^2\)
\(\Leftrightarrow IE=\sqrt{100-36}=\sqrt{64}\)
\(\Leftrightarrow IE=8\left(cm\right)\)
Mà: \(AB=IE=8\left(cm\right)\) (ABIE là hình chữ nhật)
Diện tích của tứ giác ABOI có AB là đường cao là:
\(S_{ABOI}=\dfrac{\left(IB+OA\right)\cdot AB}{2}=\dfrac{\left(2+8\right)\cdot8}{2}=40\left(cm^2\right)\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC (H thuộc BC). Gọi D,E lần lượt là hình chiếu của H trên AB, AC
CMR: BD\(\sqrt{CH}\)+ CE\(\sqrt{BH}\)= AH\(\sqrt{BC}\)
Cho x,y,z là các số dương thỏa mãn: x + y + z + \(\sqrt{xyz}\)= 4. Tính giá trị của
P = \(\sqrt{x\left(4-y\right)\left(4-z\right)}\)+ \(\sqrt{y\left(4-z\right)\left(4-x\right)}\)+\(\sqrt{z\left(4-x\right)\left(4-y\right)}\)- \(\sqrt{4yz}\)
Trên một đường thẳng (d) cho hai điểm A, B. Các đường thẳng tia Ax, By cùng nằm trong nửa mặt phẳng bờ là đường thẳng (d). Trên Ax lấy 1 điểm C, trên By lấy 1 điểm D thỏa AB2 = 4AC.BD. Vẽ các đường tròn tâm C và D và theo thứ tự, tiếp xúc với (d) tại các điểm A,B. Chứng minh : hai đường tròn đó tiếp xúc với nhau.
Cho ba đường tròn ( O, R ), ( O', R' ), ( O'', r ) cùng tiếp xúc với một đường thẳng ( d ) và tiếp xúc với nhau từng đôi một. Chứng minh rằng nếu r là bán kính đương tròn nhỏ nhất thì \(\dfrac{1}{\sqrt{r}}=\dfrac{1}{\sqrt{R}}+\dfrac{1}{\sqrt{R'}}\)
Cho nửa đường tròn tâm O đường kính AB và điểm I nằm giữa A và B. Gọi C là 1 điểm trên nửa đường tròn tâm O, đường thẳng qua C vuông góc với IC cắt các tiếp tuyến của nửa đường tròn tại A và B lần lượt là M và N
Chứng minh ∆CAI~∆CBN
Chứng minh góc MIN=90 độ












