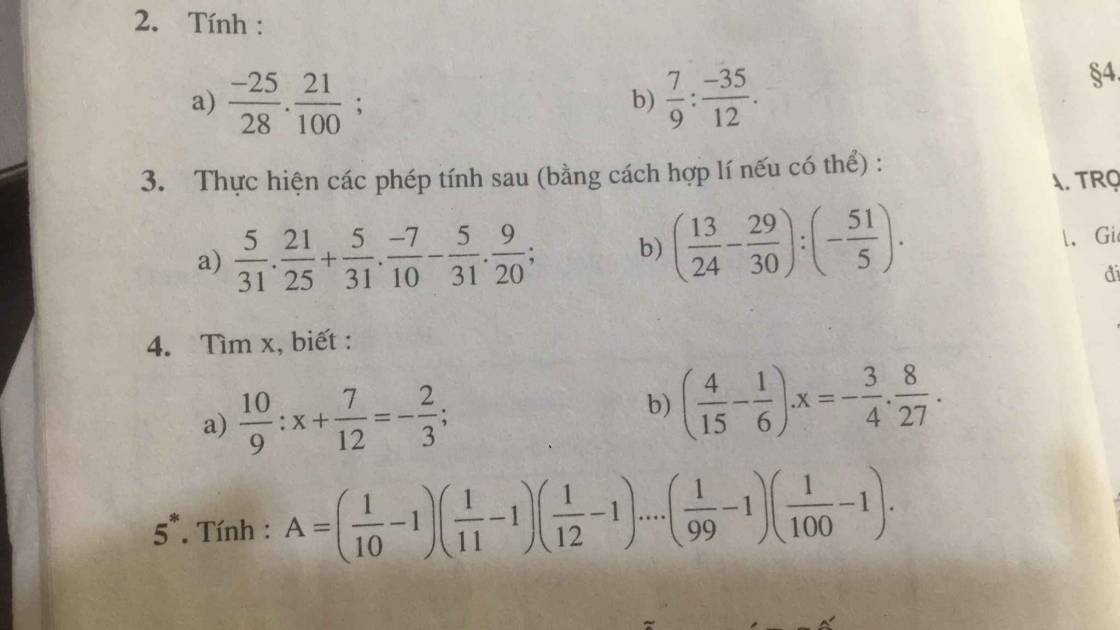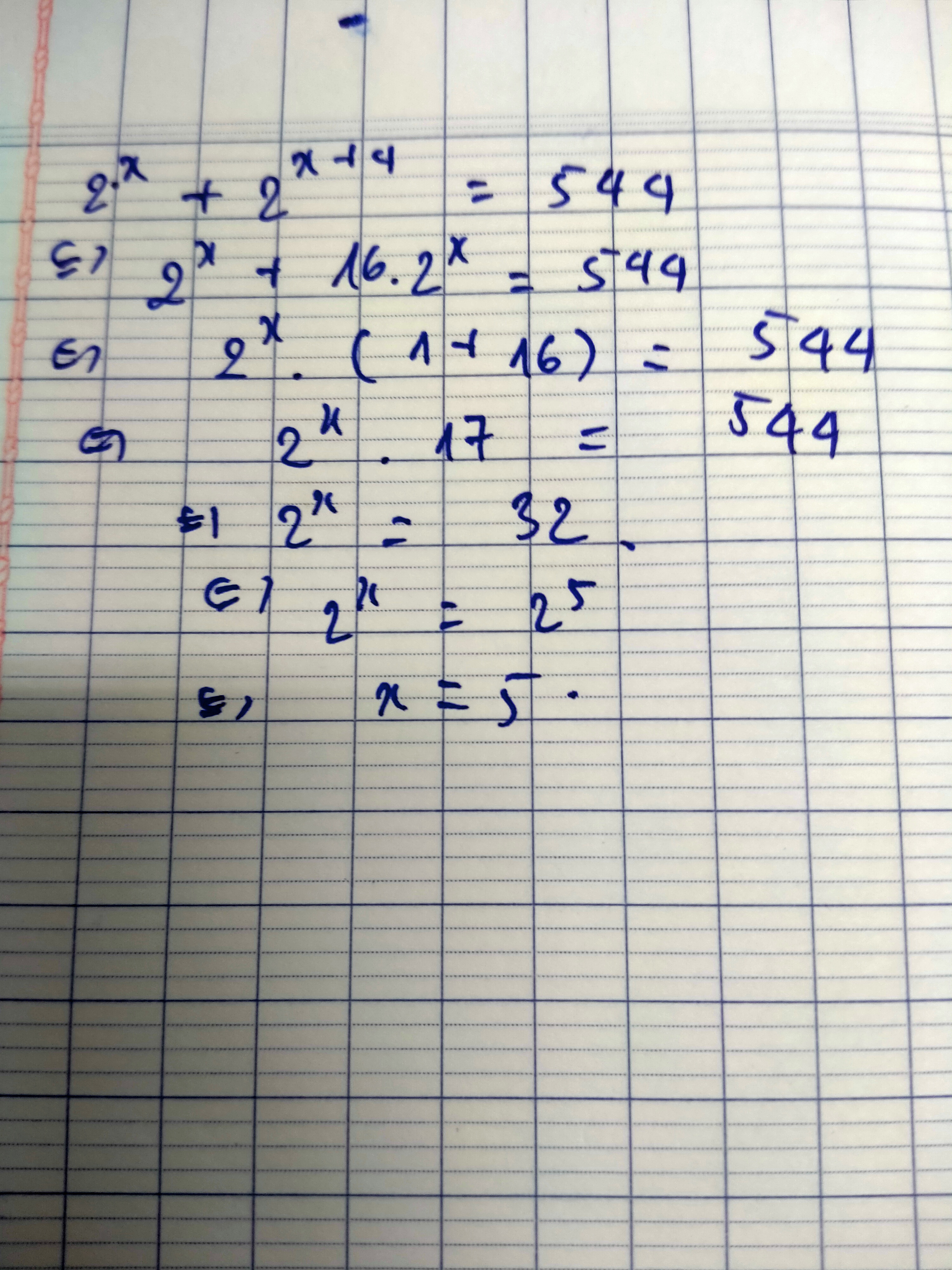Bài 3: Nhân, chia số hữu tỉ

\(\left(4x^2-3\right)^3+8=0\)

\(\left(4x^2-3\right)^3=-8\\ =>4x^2-3=-2\)

\(4x^2=1\\ x^2=\dfrac{1}{4}=>\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Bài 2:

a)

\(\dfrac{-25}{28}\)x\(\dfrac{21}{100}\)

=\(\dfrac{-525}{2800}\)=\(\dfrac{-3}{16}\)

b)

\(\dfrac{7}{9}\):\(\dfrac{-35}{12}\)

=\(\dfrac{7}{9}\)x\(\dfrac{-12}{35}\)

=\(\dfrac{-84}{315}\)=\(\dfrac{-4}{15}\)

Làm những bài nào vậy cậu?

Đề bài yêu cầu gì?

Chụp tách ra bn!

=-4/5(25+3/19-35-3/19)

=-4/5*(-10)

=8

\(25\dfrac{3}{19}:\left(-\dfrac{5}{4}\right)-35\dfrac{3}{19}:\left(-\dfrac{5}{4}\right)\\ =\left(25\dfrac{3}{19}-35\dfrac{3}{19}\right):\left(-\dfrac{5}{4}\right)\\ =-10:\left(-\dfrac{5}{4}\right)\\ =8\)

\(2^x+2^{x+4}=544\\\Rightarrow2^x\cdot1+2^x\cdot2^4=544\\\Rightarrow2^x\cdot(1+2^4)=544\\\Rightarrow2^x\cdot(1+16)=544\\\Rightarrow2^x\cdot17=544\\\Rightarrow2^x=544:17\\\Rightarrow2^x=32\\\Rightarrow2^x=2^5\\\Rightarrow x=5\)

\(2^x+2^{x+4}=544\)

=>\(2^x+2^x\cdot2^4=544\)

=>\(2^x\left(1+2^4\right)=544\)

=>\(2^x\cdot17=544\)

=>\(2^x=\dfrac{544}{17}=32\)

=>\(2^x=2^5\)

=>x=5

ae giup coi

 ai giúp coi

giúp nhanh lên

8 h học

(x-5)^2*x=(x-5)

=>(x-5)[x(x-5)-1]=0

=>(x-5)(x^2-5x-1)=0

=>x=5 hoặc x^2-5x-1=0

=>\(x\in\left\{5;\dfrac{5\pm\sqrt{29}}{2}\right\}\)

a> Để A là số nguyên thì x-2+5 chia hết cho x-2

=>\(x-2\in\left\{1;-1;5;-5\right\}\)

hay \(x\in\left\{3;1;7;-3\right\}\)

b: Để B là số nguyên thì -2x-6+7 chia hết cho x+3

=>\(x+3\in\left\{1;-1;7;-7\right\}\)

hay \(x\in\left\{-2;-4;4;-10\right\}\)

`C=1/(-2021) -1/(-2019) +1/(-2019) -1/(-2017) +...+1/(-3) -1/(-1)`

`C=(-1)/2021 +1=2022/2021`