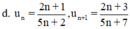
với n ∈ N*, n ≥ 1
Xét:
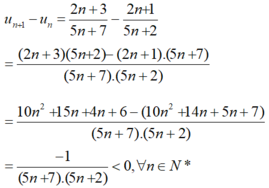
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm
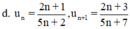
với n ∈ N*, n ≥ 1
Xét:
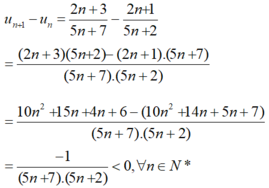
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
xét tính tăng, giảm của các dãy số sau
\(u_n=\dfrac{n+2}{n}\)
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2-3n\)
b) \(u_n=\dfrac{n+1}{n}\)
c) \(u_n=\dfrac{1}{n+1}\)
d) \(u_n=2^n\)
Xét tính tăng, giảm của các dãy số u n , biết: u n = n - 1 n + 1
Xét tính tăng giảm của dãy số: un = \(\dfrac{3^n-1}{2^n}\)
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2n-1\)
b) \(u_n=3-2n\)
c) \(u_n=\dfrac{n+2}{n}\)
d) \(u_n=\dfrac{2}{n}\)
e) \(u_n=3^n\)
Xét tính tăng giảm và bị chặn của các dãy số sau: u 1 = 2 ; u 2 = 3 u n + 1 = u n + u n - 1 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
Xét tính tăng - giảm của dãy số (un) với
a) un=\(\dfrac{3^n}{2^{n+1}}\)
b) un=\(\dfrac{3^n}{n^2}\)
c) un=\(\sqrt{n}-\sqrt{n-1}\)
Xét tính tăng giảm của dãy số: un = \(\sqrt{n+10}-\sqrt{n+2}\)