1: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
2: Ta có: \(\widehat{BFE}+\widehat{BCE}=180^0\)
mà \(\widehat{BFE}+\widehat{MFB}=180^0\)(hai góc kề bù)
nên \(\widehat{MFB}=\widehat{MCE}\)
Xét ΔMFB và ΔMCE có
\(\widehat{MFB}=\widehat{MCE}\)
\(\widehat{FMB}\) chung
Do đó: ΔMFB~ΔMCE
=>\(\dfrac{MF}{MC}=\dfrac{MB}{ME}\)
=>\(MF\cdot ME=MB\cdot MC\)

















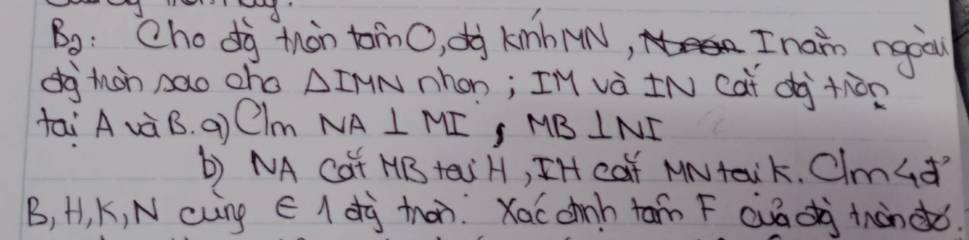

 vẽ hình luôn ạ
vẽ hình luôn ạ
