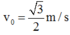Từ đỉnh của một tòa nhà cao h = 25 m, người ta ném một quả bóng lên cao với vận tốc ban đầu v, = 15 m/s?, theo phương nghiêng một góc a = 45° so với phương ngang.
Hãy thiết lập phương trình chuyển động và phương trình quỹ đạo của quả bóng.Tính thời gian quả bóng rơi từ đỉnh tháp xuống mặt đất.Tính tầm xa (theo phương ngang) của quả bóng.Tính vận tôc, gia tốc tiếp tuyến và pháp tuyến của quả bóngĐầu tiên chọn hệ trục toạ độ gốc tại điểm ném, trục OX theo phương ngang, trục OY thẳng đứng hướng lên. Vận tốc ban đầu v0 = 15 m/s, góc ném α = 45°, chiều cao ban đầu h = 25 m. Thành phần vận tốc: • v0x = v0⋅cosα = 15⋅ 0,707 ≈ 10,6 m/s (không đổi trong quá trình chuyển động). • v0y = v0⋅sinα = 15⋅ 0,707 ≈ 10,6 m/s. 1. Phương trình chuyển động theo thời gian: x(t) = v0x⋅t = 10,6·t ; y(t) = h + v0y⋅t – 0,5⋅g⋅t² = 25 + 10,6⋅t – 4,9⋅t² (với g ≈ 9,8 m/s²). 2. Phương trình quỹ đạo (loại t): Thay t = x/v0x vào y(t) thu được: y(x) = h + x⋅tanα – (g⋅x²)/(2⋅v0²⋅cos²α) = 25 + x⋅tan45° – (9,8⋅x²)/(2⋅ 15²⋅cos²45°). 3. Thời gian rơi xuống đất: lấy y(t) = 0, 4,9⋅t² – 10,6⋅t – 25 = 0 ⇒ t ≈ 3,59 s (nghiệm dương). 4. Tầm xa theo phương ngang: R = v0x⋅t ≈ 10,6⋅ 3,59 ≈ 38 m. 5. Vận tốc và gia tốc tiếp tuyến, pháp tuyến: Tại thời điểm t, vận tốc v→ có thành phần v_x = v0x = 10,6 m/s và v_y(t) = v0y – g⋅t = 10,6 – 9,8⋅t. Độ lớn vận tốc: v = √[v_x² + v_y^2]. Gia tốc luôn hướng thẳng đứng xuống nên có biểu thức a→ = (0; –g). Gia tốc tiếp tuyến bằng (a→⋅ v→)/v còn gia tốc pháp tuyến bằng √(a^2 – a_t^2). Khi vật chạm đất (t ≈ 3,59 s) thì v_y ≈ −24,6 m/s nên |v| ≈ 26,8 m/s.