Đường thẳng vuông góc với mặt \(x+2y-2z-3=0\) nên nhận \(\left(1;2;-2\right)\) là 1 vtcp
Do đó đường thẳng có pt:
\(\dfrac{x-1}{1}=\dfrac{y-4}{2}=\dfrac{z+7}{-2}\)
Đường thẳng vuông góc với mặt \(x+2y-2z-3=0\) nên nhận \(\left(1;2;-2\right)\) là 1 vtcp
Do đó đường thẳng có pt:
\(\dfrac{x-1}{1}=\dfrac{y-4}{2}=\dfrac{z+7}{-2}\)
Trong không gian với trục tọa độ Oxyz, cho đường thẳng
∆ : x - 1 2 = y - 1 = z + 2 3 và mặt phẳng ( α ): x-2y+2z-3=0.
Đường thẳng đi qua O, vuông góc với ∆ và song song với
mặt phẳng ( α ) có phương trình
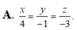
![]()
![]()
![]()
Trong không gian Oxyz, phương trình đường thẳng đi qua điểm M(1;2;-3) và vuông góc với mặt phẳng (P): x-y+2z-1=0 là
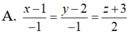
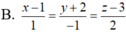
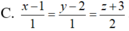
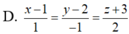
Trong không gian Oxyz, đường thẳng đi qua điểm A(-1;2;1) và vuông góc với mặt phẳng (P):x-2y-z-5=0 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng α đi qua hai điểm A(3;1;-1), B(2;-1;4) và vuông góc với mặt phẳng β : 3x+y-2z+5=0 là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm A ( 1 ; 2 ; - 2 ) , B ( 2 ; - 1 ; 4 ) và vuông góc với ( β ) : x - 2 y - z + 1 = 0 .
A. 15x + 7y + z – 27 = 0
B. 15x – 7y + z + 1 = 0
C. 15x – 7y – z + 1 = 0
D. Đáp án khác
Trong không gian Oxyz, viết phương trình đường thẳng đi qua điểm M(1;-2;3) và vuông góc với mặt phẳng (P): x+y-2z+3=0
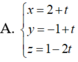
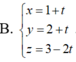
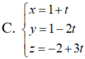
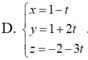
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng d đi qua điểm A(1;2;1) và vuông góc với mặt phẳng (P): x-2y+z-1=0 có dạng
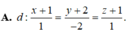
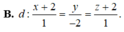
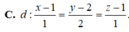
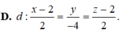
Trong không gian với hệ tọa đọ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng ∆ có phương trình x - 2 1 = y - 1 1 = z 2 và vuông góc với mặt phẳng β : x + y - 2 z + 1 = 0 . Giao tuyến của (α) và (β) đi qua điểm nào trong các điểm sau:
A. A (2;1;1)
B. C (1;2;1)
C. D (2;1;0)
D. B(0;1;0)
Trong không gian Oxyz, hãy viết phương trình của đường thẳng d đi qua điểm M(-1;0;0) và vuông góc với mặt phẳng (P): x+2y-z+1=0.
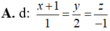
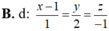
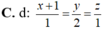
![]()
Trong không gian toạ độ Oxyz, cho mặt phẳng (P): x-2y+z-3=0 và điểm A(1;2;0). Viết phương trình đường thẳng qua A và vuông góc với (P).
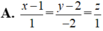
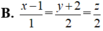
![]()
![]()