Phương pháp:
Sử dụng phương pháp đổi đỉnh
Cách giải:

Phương pháp:
Sử dụng phương pháp đổi đỉnh
Cách giải:


Cho hình chóp SABC có tam giác ABC vuông tại A, AB=AC=a. I là trung điểm của SC.Hình chiếu vuông góc của S lên mp (ABC) là trung điểm H của BC , mp (SAB) tạo với đáy một góc 60. Tính thể tích khối chóp SABC và khoảng cách từ I tới mp (SAB) theo a
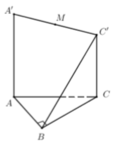
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB = a, AA' = 2a. Gọi M là trung điểm của đoạn thẳng A'C', I là giao điểm của AM và A'C. Tính khoảng cách từ điểm A đến mặt phẳng (IBC).
A. 2 5 a 5 .
B. 5 a 5 .
C. 2 3 a 5 .
D. 3 a 5 .
Cho tam giác ABC có AB = 3a, đường cao CH = a và AH = a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A', B', C' sao cho AA' = 3a, BB' = 2a, CC' = a. Tính diện tích tam giác A'B'C'.
A. a 2 39 3 .
B. a 2 21 3 .
C. a 2 26 2 .
D. a 2 35 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC = 2a, BC = a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 ° . Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mặt phẳng (ABC) và nằm cùng một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B',C' sao cho BB' = a, CC' = 2a. Tính cosin góc giữa hai mặt phẳng (ABC) và (A'B'C').
A. 30 10
B. 15 10
C. 14 10
D. 42 14
Trong không gian tọa độ Oxyz cho sáu điểm A(2;0;0), A’(6;0;0), B(0;3;0), B’(0;4;0), C(0;0;3), C’(0;0;4). Tính côsin của góc giữa hai mặt phẳng mp(ABC) và mp(A'B'C').
A. cos φ = 18 375
B. cos φ = 18 374
C. cos φ = 18 376
D. cos φ = 18 377
Cho tam giác đều ABC có cạnh bằng 3a. Điểm H thuộc cạnh AC với HC = a. Dựng đoạn thẳng SH vuông góc với mặt phẳng (ABC) với SH = 2a. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng
A. 3a
B. 3 21 7 a
C. 21 7 a
D. 3 7 a
Cho tam giác đều ABC có cạnh bằng 3a. Điểm H thuộc cạnh AC với HC=a. Dựng đoạn thẳng SH vuông góc với mặt phẳng (ABC) với SH=2a. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng
A. 3 a 7
B. 3 a 21 7
C. a 21 7
D. 3 a
Cho tam giác ABC có hai đỉnh B, C cố định BC = 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là
A. Đường thẳng x+2y+4a=0
![]()
D. Parabôn y=2ax2