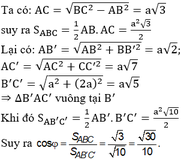Các câu hỏi tương tự
Cho tam giác ABC có AB 3a, đường cao CH a và AH a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A, B, C sao cho AA 3a, BB 2a, CC a. Tính diện tích tam giác ABC. A.
a
2
39
3
.
B.
a
2
21...
Đọc tiếp
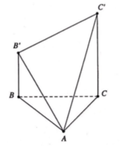
Cho tam giác ABC có AB = 3a, đường cao CH = a và AH = a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A', B', C' sao cho AA' = 3a, BB' = 2a, CC' = a. Tính diện tích tam giác A'B'C'.
A. a 2 39 3 .
B. a 2 21 3 .
C. a 2 26 2 .
D. a 2 35 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC 2a, tam giác SAB và tam giác SCB lần lượt vuông tại A, C. Khoảng cách từ S đến mặt phẳng (ABC) bằng 2a. Cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng: A.
1
3
B.
1
3
C.
1
2
D.
1
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, tam giác SAB và tam giác SCB lần lượt vuông tại A, C. Khoảng cách từ S đến mặt phẳng (ABC) bằng 2a. Cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng:
A. 1 3
B. 1 3
C. 1 2
D. 1 2
Trong mặt phẳng (P), cho hình bình hành ABCD. Vẽ các tia Bx, Cy, Dz song song với nhau, nằm cùng phía với mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A, cắt Bx, Cy, Dz tương ứng tại B’, C’, D’. Biết
B
B
2
,
D
D
4.
Tính CC A. 2 B. 8 C. 6 D. 3
Đọc tiếp
Trong mặt phẳng (P), cho hình bình hành ABCD. Vẽ các tia Bx, Cy, Dz song song với nhau, nằm cùng phía với mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A, cắt Bx, Cy, Dz tương ứng tại B’, C’, D’. Biết B B ' = 2 , D D ' = 4. Tính CC
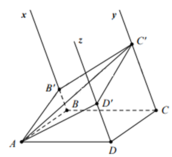
A. 2
B. 8
C. 6
D. 3
Cho hình vuông ABCD cạnh a. Trên hai tia Bx, Dy vuông góc với mặt phẳng (ABCD) và cùng chiều lấy lần lượt hai điểm M, N sao cho
B
M
a
2
,
D
N
a
.
. Tính góc
φ
giữa hai mặt phẳng
A
M
N
v
à
C
M
N...
Đọc tiếp
Cho hình vuông ABCD cạnh a. Trên hai tia Bx, Dy vuông góc với mặt phẳng (ABCD) và cùng chiều lấy lần lượt hai điểm M, N sao cho B M = a 2 , D N = a . . Tính góc φ giữa hai mặt phẳng A M N v à C M N .
A. φ = 30 ∘
B. φ = 90 ∘
C. φ = 60 ∘
D. φ = 45 ∘
Trong mặt phẳng (P) cho tam giác OAB cân tại O,
O
A
O
B
2
a
,
A
O
B
^
120
°
. Trên đường thẳng vuông góc với mặt phẳng (P) tại O lấy hai điểm C, D nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD. A. ...
Đọc tiếp
Trong mặt phẳng (P) cho tam giác OAB cân tại O, O A = O B = 2 a , A O B ^ = 120 ° . Trên đường thẳng vuông góc với mặt phẳng (P) tại O lấy hai điểm C, D nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 3 a 2 2
B a 2 3
C. 5 a 2 2
D. 5 a 2 3
Trong mặt phẳng (P) cho tam giác OAB cân tại
O
,
O
A
O
B
2
a
,
A
O
B
^
120
°
. Trên đường thẳng vuông góc với măt phẳng (P) tại O lấy hai điểm C, D , nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD. A. ...
Đọc tiếp
Trong mặt phẳng (P) cho tam giác OAB cân tại O , O A = O B = 2 a , A O B ^ = 120 ° . Trên đường thẳng vuông góc với măt phẳng (P) tại O lấy hai điểm C, D , nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 3 a 2 2
B. a 2 3
C. 5 a 2 2
D. 5 a 2 3
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy ABC là tam giác đều cạnh a, tam giác A BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC. Tính cosin góc
α
giữa hai đường thẳng AA và BM. A.
cos
α
2
22
11
B.
cos
α...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình chóp tam giác S.ABC có đáy ABC là một tam giác vuông cân tại B với trọng tâm G, cạnh bên SA tạo với đáy (ABC) một góc
30
0
. Biết hai mặt phẳng
S
B
G
v
à
S
C
G
cùng vuông góc với mặt phẳng (ABC). Tính cosin của góc giữa hai đường thẳng SA và BC. A. ...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là một tam giác vuông cân tại B với trọng tâm G, cạnh bên SA tạo với đáy (ABC) một góc 30 0 . Biết hai mặt phẳng S B G v à S C G cùng vuông góc với mặt phẳng (ABC). Tính cosin của góc giữa hai đường thẳng SA và BC.
A. 15 5
B. 3 15 20
C. 15 10
D. 30 20
Trong mặt phẳng (α) cho hình vuông ABCD cạnh a. Các tia Bx và Dy vuông góc với mặt phẳng (α) và cùng chiều. Các điểm M và N lần lượt thay đổi trên Bx, Dy sao cho mặt phẳng (MAC) và (NAC) vuông góc với nhau. Khi đó tích BM.DN bằng A.
2
a
2
3
.
B.
a
2
6
.
C.
a...
Đọc tiếp
Trong mặt phẳng (α) cho hình vuông ABCD cạnh a. Các tia Bx và Dy vuông góc với mặt phẳng (α) và cùng chiều. Các điểm M và N lần lượt thay đổi trên Bx, Dy sao cho mặt phẳng (MAC) và (NAC) vuông góc với nhau. Khi đó tích BM.DN bằng
A. 2 a 2 3 .
B. a 2 6 .
C. a 2 3 .
D. a 2 2 .