Đáp án B
Gọi 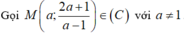 với a
≢
1.
với a
≢
1.
Ta có 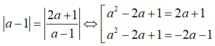
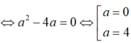
Vậy điểm cần tìm là: ![]() .
.
Đáp án B
Gọi 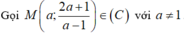 với a
≢
1.
với a
≢
1.
Ta có 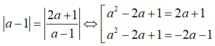
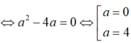
Vậy điểm cần tìm là: ![]() .
.
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = x + 2 x - 2 cách đều hai đường tiệm cận của (C) là
A.![]()
B. ![]()
C. 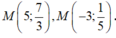
D. ![]()
Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y = x + 2 x - 2 sao cho tổng khoảng cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là
A.![]()
B. ![]()
C.![]()
D.![]()
Tọa độ các điểm thuộc đồ thị (C) của hàm số y = 3 x - 5 x - 2 cách đều hai tiệm cận của (C).
A. ![]()
B. ![]()
C.![]()
D.![]()
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = 2 x - 1 x - 1 sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 1 là
A. ![]()
B. ![]()
C. 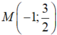
D. 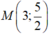
Tọa độ tất cả các điểm thuộc đồ thị (C) của hàm số y = x + 1 x - 2 sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất là
A. (1;1)
B.![]()
C. ![]()
D. ![]()
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = x + 3 x - 1 cách đều hai trục tọa độ là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tọa độ các điểm thuộc đồ thị (C) của hàm số y = 2 x + 1 x - 1 mà có tổng khoảng cách đến hai đường tiệm cận của (C) bằng 4 là
A.![]()
B. ![]()
C.![]()
D. ![]()
Cho đồ thị (C) của hàm số y = x - 3 x + 1 Điểm M nào dưới đây thuộc đồ thị (C) và cách đều hai trục tọa độ
A.![]()
B.![]()
C.![]()
D. ![]()
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN.
A.![]()
B. MN = 3
C. ![]()
D. ![]()