Đáp án A
Gọi
 với
a
≢
1
.
với
a
≢
1
.
Tiệm cận đứng của (C) là x-1.
Ta có 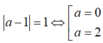 . Vậy
. Vậy ![]() .
.
Đáp án A
Gọi
 với
a
≢
1
.
với
a
≢
1
.
Tiệm cận đứng của (C) là x-1.
Ta có 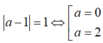 . Vậy
. Vậy ![]() .
.
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C).
A. 0
B. 3
C. 2
D. 1
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y = x + 2 x - 2 sao cho khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần
khoảng cách từ M đến tiệm cận đứng?
A. 2.
B. 1
C. 3.
D. 4.
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Đồ thị (C) của hàm số y = x + 2 x - 3
Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y = x + 2 x - 2 sao cho tổng khoảng cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là
A.![]()
B. ![]()
C.![]()
D.![]()
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
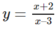
b) Chứng minh rằng giao điểm I của hai tiệm cận của (C) là tâm đối xứng của (C).
c) Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Tọa độ tất cả các điểm thuộc đồ thị (C) của hàm số y = x + 1 x - 2 sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất là
A. (1;1)
B.![]()
C. ![]()
D. ![]()
Tọa độ điểm M thuộc đồ thị (C) của hàm số 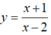 mà có khoảng cách đến tiệm cận ngang của (C) bằng 1 là
mà có khoảng cách đến tiệm cận ngang của (C) bằng 1 là
A.![]()
B.![]()
C. ![]()
D. 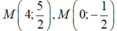
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Tổng khoảng cách từ một điểm M thuộc (C) đến hai tiệm cận của (C) đạt giá trị nhỏ nhất
bằng
A. 3.
B. 4.
C. 2 2
D. 2
Tọa độ các điểm thuộc đồ thị (C) của hàm số y = 2 x + 1 x - 1 mà có tổng khoảng cách đến hai đường tiệm cận của (C) bằng 4 là
A.![]()
B. ![]()
C.![]()
D. ![]()