từ 6/3/2016 đến giờ 3 cau tl mà k có lời giải, chắc bn Duy buồn lắm
stron = πr2
svuong = 2r2
ta có: πr2 - 2r2 = 3,42 => r2 = 3cm
svuong = 2r2 = 2.3 = 6cm2
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A ' B ' C ' D ' có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S x q = 13 πa 2 4
B. S x q = 13 πa 2 12
C. S x q = 37 πa 2 4
D. S x q = 37 πa 2 12
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S xq = 13 πa 2 4
B. S xq = 37 πa 2 12
C. S xq = 13 πa 2 12
D. S xq = 37 πa 2 4
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 ° . Tính diện tích toàn phần S t p của hình chóp S.ABCD
A. S t p = a 2 7
B. S t p = a 2 1 + 7
C. S t p = a 2 4 + 7 4
D. S t p = a 2 7 4
Cho hình tròn tâm O và hai đường kình AB và BD vuông góc với nhau. Biết diện tích hình vuông ABCD là 120 cm vuông. Tính diện tích hình tròn tâm O
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng 3a. Một hình nón có đỉnh S và đáy là hình tròn ngoại tiếp hình vuông ABCD Diện tích xung quanh của hình nón bằng
A. 3 2 π a 2
B. 3 2 π a 2 2
C. 6 π a 2
D. 6 2 π a 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên S A = a 6 và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
A. 8 πa 2
B. 2 πa 2
C. 2 a 2
D. a 2 2
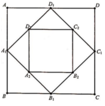
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3,…và cứ thế tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100 (tham khảo hình bên). Tính tổng S = S1 + S2 + S3 + … + S100
A. S = a 2 2 100 - 1 2 100
B. S = a 2 2 100 - 1 2 99
C. S = a 2 2 100
D. S = a 2 2 99 - 1 2 98
