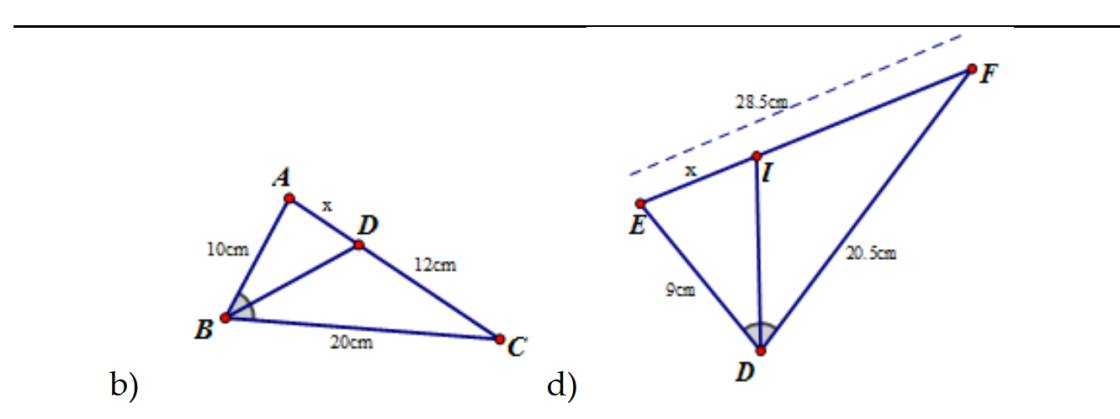
b: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{10}=\dfrac{12}{20}=\dfrac{3}{5}\)
=>\(AD=\dfrac{3}{5}\cdot10=6\left(cm\right)\)
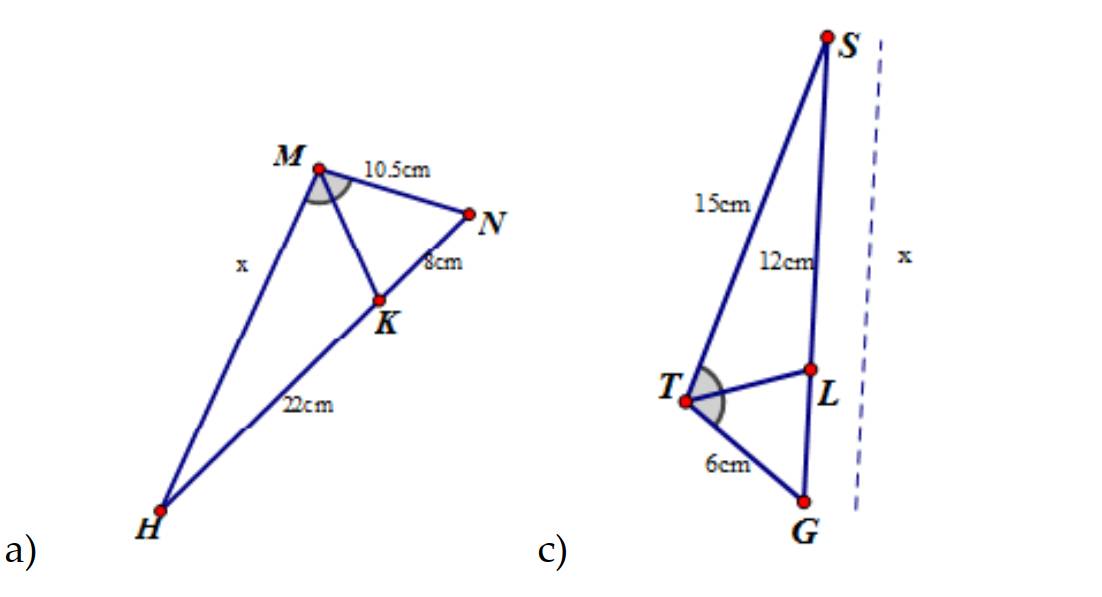
a: Xét ΔMHN có MK là phân giác
nên \(\dfrac{KN}{KH}=\dfrac{MN}{MH}\)
=>\(\dfrac{10.5}{x}=\dfrac{8}{22}=\dfrac{4}{11}\)
=>\(x=10.5\cdot\dfrac{11}{4}=28,875\left(cm\right)\)
c: Xét ΔTSG có TL là phân giác
nên \(\dfrac{LG}{TG}=\dfrac{LS}{TS}\)
=>\(\dfrac{LG}{LS}=\dfrac{TG}{TS}=\dfrac{6}{15}=\dfrac{2}{5}\)
=>\(\dfrac{LG}{12}=\dfrac{2}{5}\)
=>LG=12*2/5=4,8(cm)
x=GS=GL+LS=4,8+12=16,8(cm)
d: Xét ΔDEF có DI là phân giác
nên \(\dfrac{EI}{DE}=\dfrac{IF}{DF}\)
=>\(\dfrac{EI}{9}=\dfrac{IF}{20,5}\)
mà EI+IF=EF=28,5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{EI}{9}=\dfrac{IF}{20,5}=\dfrac{EI+IF}{9+20,5}=\dfrac{28.5}{29.5}=\dfrac{57}{59}\)
=>\(EI=\dfrac{57}{59}\cdot9=\dfrac{513}{59}\left(cm\right)\)
=>\(x=\dfrac{513}{59}\left(cm\right)\)