Các câu hỏi tương tự
Cho hàm số f thỏa mãn
f
cot
x
sin
2
x
+
cos
2
x
,
∀
x
∈
0
;
π
. Giá trị lớn nhất của hàm số
g
x
f
sin
2
x
.
f...
Đọc tiếp
Cho hàm số f thỏa mãn f cot x = sin 2 x + cos 2 x , ∀ x ∈ 0 ; π . Giá trị lớn nhất của hàm số g x = f sin 2 x . f cos 2 x trên ℝ là
A. 6 125 .
B. 1 20 .
C. 19 500 .
D. 1 25 .
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Cho hàm số y f (x) liên tục trên
ℝ
và có đồ thị như hình vẽ bên.Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) m có nghiệm thuộc khoảng (0;
π
) là A. [-1;3) B. (-1;1) C. (-1;3) D. [-1;1 )
Đọc tiếp
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
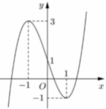
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f
f
sin
x
m
có nghiệm thuộc khoảng
0
;
π
? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình f f sin x = m có nghiệm thuộc khoảng 0 ; π ?
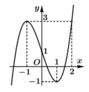
A. 2
B. 3
C. 4
D. 5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
(
x
)
2
c
o
s
3
x
-
c
o
s
2
x
trên đoạn D[
-
π
/
3
;
π
/
3
] A.
m
a
x
(
x
∈...
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 c o s 3 x - c o s 2 x trên đoạn D=[ - π / 3 ; π / 3 ]
A. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
B. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = - 3
C. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = - 3
D. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
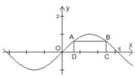
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hàm số
y
f
x
liên tục trên
ℝ
và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
f
sin
x
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng A. -10 B. -8 C. -...
Đọc tiếp
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng
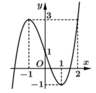
A. -10
B. -8
C. -6
D. -5
Tập xác định của hàm số
(
x
2
-
3
x
+
2
)
π
là: A. R{1;2} B. (1;2) C.
(
-
∞
;
1
]
∪
[
2
;
+
∞
)
D.
-
∞
;
1
∪
2
;...
Đọc tiếp
Tập xác định của hàm số ( x 2 - 3 x + 2 ) π là:
A. R\{1;2}
B. (1;2)
C. ( - ∞ ; 1 ] ∪ [ 2 ; + ∞ )
D. - ∞ ; 1 ∪ 2 ; + ∞
Tập xác định của hàm số
(
x
2
-
3
x
+
2
)
π
là A.
R
{
1
;
2
}
B.
(
-
∞
;
1
)
∪
(
2
;
+
∞
)
C.
(
1...
Đọc tiếp
Tập xác định của hàm số ( x 2 - 3 x + 2 ) π là
A. R \ { 1 ; 2 }
B. ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
C. ( 1 ; 2 )
D. ( - ∞ ; 1 ] ∪ [ 2 ; + ∞ )
Tập xác định của hàm số
y
2
x
−
x
2
−
π
là A.
0
;
2
B.
−
∞
;
0
∪...
Đọc tiếp
Tập xác định của hàm số y = 2 x − x 2 − π là
A. 0 ; 2
B. − ∞ ; 0 ∪ 2 ; + ∞
C. − ∞ ; 0 ∪ 2 ; + ∞
D. 0 ; 2




