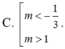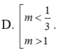Đặt \(t=3^{\log_2x}\)
\(Pt\Leftrightarrow t^2-2\left(m+3\right)t+m^2+3\left(1\right)\)
Ta có : \(t=3^{\log_2x}\Rightarrow x=2^{\log_3t}\)
\(\Rightarrow x_1.x_2=2^{\left(\log_3t_1+\log_3t_2\right)}=2^{\log_3\left(t_1.t_2\right)}\)
\(\)\(x_1.x_2>2\Rightarrow2^{\log_3\left(t_1.t_2\right)}>2\Rightarrow\log_3\left(t_1.t_2\right)>1\Rightarrow t_1.t_2>3\)
Để phương trình có 2 nghiệm phân biệt \(x_1.x_2>2\) khi và chỉ khi (1) có 2 nghiệm phân biệt dương và \(t_1.t_2>3\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=6m+6>0\\S=2\left(m+3\right)>0\\P=m^2+3>0\\P=m^2+3>3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m>-3\\m\ne0\end{matrix}\right.\) \(\Leftrightarrow m>-1\cap m\ne0\)
Vậy với \(m>-1\cap m\ne0\) thỏa mãn đề bài