- Ta có:
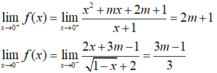
- Hàm số có giới hạn khi x → 0 khi và chỉ khi:
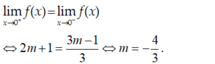
Chọn D.
- Ta có:
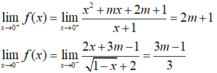
- Hàm số có giới hạn khi x → 0 khi và chỉ khi:
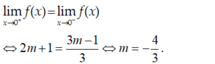
Chọn D.
cho hàm số f(x)=\(x^2-4x+3\)
tìm gtri tham số m để \(\left|f\left(\left|x\right|\right)-1\right|=m\) có 8 nghiệm phân biệt
đáp án:
A. \(m< 1\)
B.\(0\le x\le2\)
C.1<x<2
D.0<x<1
Tìm m để các hàm số y = (m – 1)x3 – 3(m + 2)x2 – 6(m + 2)x + 1 có y’ ≥ 0, ∀ x ∈ R.
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. m ≥ 4 2
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y' ≥ 0 ∀x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. Không có giá trị nào thỏa mãn
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y ' ≥ 0 , ∀ x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. đáp án khác
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y ' ≥ 0 ∀ ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. Đáp án khác
F(x) = \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\left(x\ne1\right)\\3x+m\left(x=1\right)\end{matrix}\right.\)
Tại x0=1. Tìm m để hàm số liên tục tại x0=1
Cho biểu thức $f\left( x \right)=\dfrac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}-\left( 2m-10 \right)x-1$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để ${f}'\left( x \right)>0$ $\forall x\in \mathbb{R}$.
cho hàm số y= \(\dfrac{1}{3}x^2\)-\(\dfrac{m}{2}+mx+5\)
tìm tất cả các giá trị của tham số m để y'≥0 ∀x∈R
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1
Cho f(x)=\(-x^2+\left(2\sqrt{m}-1\right)x-m+\sqrt{m}\)
a)tìm m để f(x) >=0 vô nghiệm(lớn hơn = 0)
b)tìm m để f(x) >=0 với mọi x thuộc [1;2]