- Ta có:
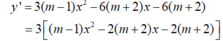
- Do đó y' ≥ 0 ∀x ∈ R(1).
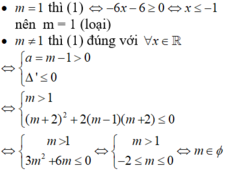
- Vậy không có giá trị nào của m thỏa mãn.
Chọn D.
- Ta có:
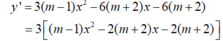
- Do đó y' ≥ 0 ∀x ∈ R(1).
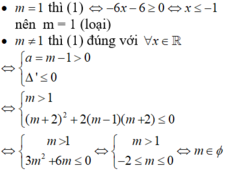
- Vậy không có giá trị nào của m thỏa mãn.
Chọn D.
Tìm m để các hàm số y = (m – 1)x3 – 3(m + 2)x2 – 6(m + 2)x + 1 có y’ ≥ 0, ∀ x ∈ R.
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. m ≥ 4 2
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y' ≥ 0 ∀x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. Không có giá trị nào thỏa mãn
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y ' ≥ 0 , ∀ x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. đáp án khác
cho hàm số y= \(\dfrac{1}{3}x^2\)-\(\dfrac{m}{2}+mx+5\)
tìm tất cả các giá trị của tham số m để y'≥0 ∀x∈R
tìm các giá trị của m để hàm số sau
a) \(y=-x^3-\left(m+1\right)x^2+3\left(m+1\right)x\) nghịch biến trên R
b) \(y=-\dfrac{1}{3}x^3+mx^2-\left(2m+3\right)x\) nghịch biến trên R
Cho y=1/3(m-1)x³-(m-1)x²+(m+3)x-2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dấu b)y'=0 có 2 nghiệm thoả mãn x1²+x2²=4
tìm các giá trị của m để hàm số sau
a) \(y=-x^3+\left(m+2\right)x^2-3x\) nghịch biến trên R
b) \(y=x^3-3x^2+\left(1-m\right)x\) đồng biến trên R
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x